弱文脈依存文法にまつわる理論言語学のはなし

<工事中>

自然言語の形態論・統語論を考えるとき、それらがどの程度「複雑」なのかを考えることは、言語理論を考えるのにも、人間の文産出・理解について考えるのにも、そして言語進化について考えるのにも極めて重要だと思います。 そして、自然言語の文法の「複雑さ」（以降、適当に「文法」といってしまいます）について、形式言語の世界では「生成力」という概念での整理がなされており、言語学研究としてきちんと扱いたいと個人的に思っています。

生成力とは？

「生成力（generative capacity）」とは、文法の「複雑さ」の概念です。 ここでの複雑さは、その文法が作る（生成する）ことのできる文字列もしくは木構造の種類をもとに定義されます。 ここで、文字列に関する生成力を「弱生成力 (weak generative capacity)」と、木構造に関する生成力を「強生成力 (strong generative capacity)」と呼びます (Chomsky, 1965; 福井・辻子, 2017; 日本語訳)。

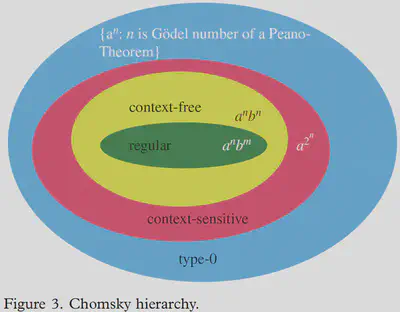
弱生成力は、ある文法が作ることのできる文字列（単語の配列）の集合に関する概念で、文法の弱生成力が等しいかつ語彙が等しい言語同士では、作ることのできる文字列の集合は完全に一致します。 つまり、弱生成力の議論において、文法とは、「容認可能な文字列のみを受理し、容認不可能な文字列は排除する装置」のことを意味します。 チョムスキー階層（下図。図はJager and Rogers (2012)より。）という概念は、弱生成力のクラス分けに関するものです（Chomsky (1956); Chomsky and Schutzenberger (1963)）。

自然言語の弱生成力の議論に関しては、Jager and Rogers (2012), Hunter (2020), Roger Levyの計算心理言語学の授業のWeek 7 あたりが良かったです。

強生成力は、ある文法が作ることのできる木構造の集合に関する概念であり、Chomsky自身は弱生成力ではなく強生成力を研究の対象とするべし、としました。 木構造は（ほぼすべての理論において）意味や韻律の理論と直接関わるので、単に容認可能な文字列を識別する装置を考えるのでは不十分だ、ということでしょう。 ただ、強生成力それ自体に明確な定義があるわけではなく、そのために理論ニュートラルな議論が難しくなっている、というのが現状です（形式言語理論の世界だと、単純にある言語クラスにおいて作ることのできる木構造の集合について考えれば良く、本来ならば、理論言語学の言語理論についても同様のことができるはずですが、残念ながら多くの言語理論は、その木構造の集合を定義することができるほど厳密ではないように思えます。もちろん、以下で紹介する範疇文法理論やMinimalist Grammarなどの形式性と記述的妥当性の両面をちゃんと追い求めている文法理論たちを除いて）。 私が知らないだけかもしれませんが、Chomskyを中心とした主流生成文法においても、強生成力の議論がなされている、というイメージはないです。

もちろん、強生成力についての議論はまったくないわけではなく、最近では、CCGとTAGが弱生成力だけではなく、強生成力においても等価である、と主張されています (Schiffer and Maletti, 2021)。 （生成力が同一となると、最後はどちらの derivation step がより妥当か、という話になる。）

文脈自由文法 (Context-Free Grammar)

自然言語の構造について考えるとき、 文脈自由文法とは、$(\Gamma, \Sigma, S, R)$ の4つ組で定義されます。

1. $\Gamma$: 非終端記号（非端末記号）の有限集合
2. $\Sigma$: 終端記号（端末記号）の有限集合で、$\Gamma\cap \Sigma=\varnothing$
3. $\mathit{S}\in \Gamma$: 開始記号
4. $R$: 規則（生成規則）の有限集合。各規則は、$\alpha\rightarrow\beta$ の形をとる。ここで、$\alpha\in\Gamma$ はちょうど1つの非終端記号、$\beta$ は $(\Gamma\cup\Sigma)^*$ の任意の列（空列を含む）であり、$\rightarrow$ は左側の要素から右側の要素への書き換えを意味します。

「文脈自由」とは、書き換え対象はただ1つの非終端記号だけであり、他の要素から影響を受ける（書き換えに文脈が存在する）というわけではないことに由来します。 これにより、ネストした構造を表現することができるので、たとえば四則演算はまさに文脈自由文法でしょう。

反復補題

ある言語が文脈自由ではないことは、以下の（文脈自由文法の）反復補題を使うことで示すことができる：

文脈自由言語 $L$ には、長さが $m$ 以上の文字列 $w$ があり、これは適当な $w, v, x, y, z\in\Sigma^*$ によって $w=uvxyz$ で表すことができる。ここで、この $w$ は以下の3つの条件を満たす：

1. 任意の $i\geq 0$ に対して、$uv^ixy^iz\in L$
2. $|vy|\geq 1$
3. $|vxy|\leq m$

例として、$L = {a^nb^nc^n\mid n\geq 0}$ が文脈自由言語であるのかこの反復補題を用いて考えてみましょう。

他の文法形式との等価性

projective dependency tree

依存構造木において、依存関係同士が「交差」しないものを projective なtreeであるといいます。 文脈自由文法で表現できる依存関係は、projectiveな依存関係にとどまることが知られています。

AB grammar

範疇文法 (Categorial Grammar) において、関数合成しかない範疇文法は、文脈自由文法とその弱生成力が等価です。

自然言語は文脈自由文法で扱えるのか？

では、自然言語の文法は、文脈自由文法で表現することはできるのでしょうか。

ここで、しょうもないですが大事な注意として、「文脈自由文法で表現することはできるのか？」という問いは、Chomsky (1957) で指摘されているように、「文法が有限個」という前提を置いた上でのものです。 というのも、観測したすべての自然言語の文を「記述」したいと思ったとき、高々それらの文と同数の文法規則さえ用意することができれば、それは、文脈自由文法どころか有限状態オートマトンで「記述」したことになります。

たとえば、projectiveな依存構造と文脈自由文法が等価ですが、依存構造が交差するとき、すなわち、non-projectiveであるとき、その構造は文脈自由文法では記述できません。 では、依存構造が交差する状況は自然言語に存在するのでしょうか？

respectively読み

こうした議論の中で、最初に（？）議論の俎上に上がったのが「respectively読み」でしょう。

図で示すように、日本語でも「それぞれ」をはさんで、主語と述語の依存関係が交差し（文字列で表すと、$a_1 b_1 a_2 b_2$ のようなコピー言語になり）、まさに文脈自由文法では記述的ないものになります。

この現象は割とわかりやすいためか、今でも時々自然言語の文脈自由文法による記述の非妥当性を示す例として紹介されがちなのですが、実は、Pullum and Gazdar (1982) により否定されています。 彼らの主張は至極単純で、respectively読みは単に統語の問題ではなく意味の問題でしょう、というものです。

Extraction

一方で、extraposition from NPやheavy NP shift、scramblingといった構文は、分析の仕方にも依りますが、非常に文脈依存性を感じるところではないでしょうか。 Extraposition from NPとは、たとえば The man fell into the pit who had been chased by dogs. のような文で、ここで、The man とそこにかかる関係節 who … の間に動詞句 fell into the pit が入っている構造です。 Scramblingは、日本語でよくある、 花子に太郎が会った。 のような、名詞句の語順が通常と入れ替わった状態のものです。

こうしたものも、Gazdar (1981) や Gazdar et al. (1985) によるGeneralized Context-Free Grammarにより記述可能であることが示されています。

Cross-serial dependency

Shieber (1985) により、Swiss-German（ドイツ語のスイス方言）の従属節中には、統語的にcross-serial dependencies（連続交差依存）が成り立ち、これにより自然言語には文脈自由文法では作れない表現が存在することが示されました。

cross-serial dependenciesとは、以下のような（ここでは連続する動詞と対応する主格の項）の依存関係が交差しあっている状況です（文は Shieber (1985) より）。

非常に雑にいうと、依存関係が交差しないネストした（入れ子構造になっている）関係だと文脈自由文法で表現できるのですが、連続交差依存は文脈自由文法では表現できません。 たとえば、高校生の頃、英語を読むときに句や節ごとに括弧でかこんで読んでいた人は多いと思うのですが（そうですよね？）、いま考えてみると、これは英語を入れ子構造として、すなわち文脈自由レベルの文法として解析していたことになります。 もしSwiss-Germanを勉強することになっていたら、このような読み方はできなかったはずです。

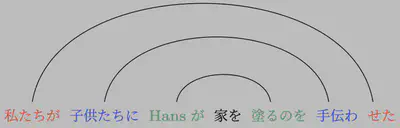
cross-serial dependenciesはそうあるわけではなく、上記の文と同じ意味を日本語で表そうとすると、以下のように、依存関係は交差せず、入れ子構造になります。 cross-serial dependencies自体は確かに頻度は多くはないですが (e.g., Ferrer i Cancho et al., 2018)、存在しないわけではないので、自然言語の文法を文脈自由文法で済ますのは不十分であるといえます。

ちなみに、同時期に Culy (1985) にて、Bambaraを用いて、形態的にも文脈自由文法で表現できない事例が存在することが示されています。
241212追記：Bambaraの例は音調的な振る舞いに依存しており、形態論の問題なのか？、という議論があるようで、結局、アイヌ語にて形態論レベルでのbeyond context-freenessが示されたようです (Sanuma and Aizawa, 2024)。

cross-serial dependency は日本語にあるのでしょうか。

また、Stabler (2004) では、英語においてもcross-serial dependenciesは存在している主張されています（画像はStabler (2004; p.701) より）。

また、正規言語で自然言語を語るのはさすがに厳しそうに思われますが、文脈自由文法は実際に自然言語の記述に広く使われています。 例えば、Penn Treebank (Marcus et al., 1993) はまさに文脈自由文法によるアノテーションであり、多言語に拡張されているところを見る限り、（実用上）大きな問題は生じていないようです。 同様に、Universal Dependencies (UD) (Nirve et al., 2020) においても、（依存関係が交差していない木をprojective、交差している木をnon-projectiveというのですが、）他言語においてもほとんどの木がprojectiveであると報告されています。つまり、UDコーパスのほとんどは文脈自由文法で記述できているということです。

自然言語は弱文脈依存言語なのか？

用語や歴史の説明は抜きにして、結論から言うと、自然言語の文法が弱文脈依存文法（Mildly Context-Sensitive Grammar; MCSG）であるということは明確に示されているわけではありません。 ただ、少なくとも以下の2つの事実から、「自然言語の文法は弱文脈依存文法である」という言説には一定の合意が得られています。そのため、しばしば弱文脈依存仮説（MCS Hypothesis）などとも呼ばれています。
なお、mildly context sensitiveという用語・概念は Joshi (1985) が初出です。

1. 文脈自由文法では表現できない構文が自然言語に存在する。

2. 数多くの（独立に提案された）文法理論が、弱文脈依存文法である。

Joshi et al. (1975) によるTree Adjoining Grammar（TAG; 木接合文法）をはじめ、多くの文法理論が、特に80-90年代にかけて、計算・数理言語学の分野で提案されましたが、そのほとんどが最終的に文脈自由文法と文脈依存文法の間にいることが示されました。 これは、多くの計算・数理言語学者の間である種の「合意」がとれた状況とも言えるでしょう。

これについては、Stabler (2013) にてわかりやすくレビューされていますので、少々長いですが引用して提示しておきます。

Stabler (2013); p.4より

In particular, a very significant computational consensus was identified by Joshi (1985) in his hypothesis that human languages are both strongly and weakly mildly context sensitive (MCS). While any empirical test of this hypothesis still depends on a network of theoretical assumptions, the claim is so fundamental that it can be connected to many diverse traditions in grammar. To say that language is "strongly and weakly" MCS is to say that MCS grammars can both define the sentences of human languages (weak adequacy) and also provide the structures of those languages (strong adequacy). Joshi’s original definition of MCS grammars was partly informal, so there are now various precise versions of his claim. One is that human languages are defined by tree adjoining grammars (TAGs) or closely related grammars, and another theoretically weaker (and hence empirically stronger) position is that human language are definable by the more expressive (set local) multi-component TAGs or closely related grammars. The most remarkable thing about this claim came out of the innocent-sounding phrase "or closely related grammars," because it was discovered that a wide range of independently proposed grammar formalisms falls under that description. In particular, a series of papers beginning in the 1980’s and 1990’s established the following inclusion relations among the languages defined by various kinds of grammars, across traditions: CFG ⊂ CCG = TAG ⊂ MCTAG = ACG = MCFG = MG ⊂ CSG

上記引用にて、

• CFGはContext-Free Grammar（文脈自由文法）
• CCGはCombinatory Categorial Grammar（組合せ範疇文法; Ades and Steedman (1982); Steedman (1996)）
• TAGはTree Adjoining Grammar（木接合文法; Joshi et al. (1975)）
• MCTAGはMulti-Component Tree Adjoining Grammar（Joshi (1987)）
• ACGはAbstract Categorial Grammar（de Groote (2001)）
• MCFGはMultiple Context Free Grammar（多重文脈自由文法; Seki et al. (1991)）
  • MCFGはLCFRS（Linear Context Free Rewriting System; Vijay-Shanker et al. (1987)）と同一。
• MGはMinimalist Grammar（Stabler (1997); Stabler (2011)）
• CSGはContext Sensitive Grammar（文脈依存文法）

を指します（定訳があるものは定訳を、また、その文法が提案されている代表的な論文情報を付与しています）。

また、このほかにも、

• Linear Indexed Grammar（LIG; Pollard (1984)）
• Head Grammar（HG; Gazdar (1985)）

も、弱文脈依存文法の仲間であることが示されています (Vijay-Shanker and Weir, 1994)。

ただ、ここで面白いのは、弱文脈依存文法は一枚岩ではなく、上記の Stabler (2013) の引用の最後の関係式で表されているように、2つのクラスに分類できます。 具体的に、CCG, TAG, LIG, HGと、MCTAG, ACG, MCFG, LCFRS, MGです（MGにも複数の亜種があります）。

その後の議論については、たとえば Stanojevic and Steedman (2020) や Frank and Hunter (2021) なども。

もちろん、各文法理論内でも、「どのような操作を仮定するか」で揺れはあるので、上記の関係が必ずしも成り立つとは限りません。たとえばCCGは、slash-typingを導入することで（＝組合せ規則の適用に制限をかけることで）、TAGよりも弱生成力が低くなることも示されています (Kuhlmann et al., 2015)。

また、Head-driven Phrase Structure Grammar (HPSG; Pollard and Sag (1994)) やType Logical Grammar (TLG; 適切な引用がわからないのでSEPへ) のような、チューリング完全な文法理論もあります。

多重文脈自由文法 (Multiple Context-Free Grammar)

弱文脈依存文法の心理的妥当性

上記のような議論ほど有名ではありませんが、最近では、計算心理言語学の分野においても、弱文脈依存文法 (MCSG) の文脈自由文法 (CFG) に対する優位性は主張されています。 たとえば、Brennan et al. (2016) や Li and Hale (2019) はMGとCFGを比較して、Stanojevic et al. (2023) はCCGとCFGを比較して、それぞれMCSGであるMG, CCGの方が、CFGよりも適切に、人が物語を聞いている間のBOLD信号（Blood Oxygen Level Dependent signals; 脳活動を反映した信号）を予測できることを示しました。

もちろん、Hale et al. (2022) で指摘されているように、こうした結果は必ずしもMCSGが uniquely the right theory of human grammar (Hale et al., 2022; p.12) であるということを意味しているわけではありませんが、MCSGが、人間の文処理に関して、CFGでは説明できていないところを説明できているのは確かです。

おわりに：

個人的には、CCGやMGによる人間の文処理のモデリング研究から計算言語学・計算心理言語学の勉強を始めた人間なので、弱文脈依存仮説は「記述研究で示されているのならそういうもの」と理解して、それから「ではなぜ自然言語は弱文脈依存なのか？」ということを考えています。が、言語を使用する際には（プッシュダウン）オートマトンっぽく使っているなぁ、正規言語〜文脈自由文法っぽく理解しているなぁという直感や、cross-serialは必ずしも処理が難しいとは限らない (Bach et al., 1986) という事実、non-projectivityは処理のしやすさである程度説明できるかもしれないが、すべてではない、というモデリング研究の進展 (Yadav et al., 2022) を見ると、もっと使用の観点から文法の複雑さについて考えないといけないよなぁとか、そもそもここでの「文法の複雑さ」はどれだけ意味のある見方なのかなぁなんて思うときはあります。

というのも、生成力は「最悪のケース」に関する議論である一方、人間の逐次的な処理における「複雑さ」は人間の記憶や予測における平均的な認知負荷を捉えており、長距離依存などはある程度複雑な文法による解析が必要ですが、たとえば日本語の助動詞などは正規言語でも解析可能である、という事実を考えると、自然言語の文法に関する議論を必ずしも最悪のケースから考えないでもいいよな、もっと平均的な処理負荷の観点から再検討すべきだよな、とは直感的に考えています（といったことは、『自然言語処理』の学会記事 (to appear) にもちょっと書きました）。 そういう意味で、認知のベイジアンモデリング (Bayesian modeling of cognition) や、情報理論によるコミュニケーションのモデル化における合理性 (rationality) に魅力を感じています。 ので、博士課程ではゆっくり時間をかけて考えながら取り組んでみたいな、とは（現時点では）考えています。