確率・情報理論を使った言語研究

Mar 3, 2025

確率や情報理論といった数学の道具は、言語使用や言語の構造それ自体を支配している何らかの規則を記述するのに非常に有用であるように思えます。

それは、確率や情報理論といったものは現象に対して理論中立的 (theory-neutral) な記述が可能で、とにかく使い勝手が良い道具だからなのかもしれないし、そもそも人間の言語処理をはじめとした認知活動が何らかの確率的なものだからなのかもしれないし、認知活動自体が、ベイジアンが主張するような「合理的 (rational)」なものだと考えたら合理的でありそう、という直感や経験的事実があるからなのかもしれないし…。

いずれにせよ、確率や情報理論は、言語処理・言語使用の研究（つまり、Performance の側面の研究）、そしてさらには言語の構造や知識自体の研究（つまり、Competence の側面）をするのに非常に強力な道具です。

近年は、コーパスをはじめとした言語資源の整備、計算機の性能向上やプログラミング言語・各種計算ライブラリの充実、大規模言語モデルのような汎用的な言語処理技術たちの登場によりかなりの精度で言語の情報量が推定できるようになってきたこと、といったさまざまな要因たちが揃ってきて、そしてさらには、確率や情報理論といった道具自体の理論研究や言語研究へ応用するといった方法論が確立されてきたので、これからできることが大量にあるよ、という状況です。

実際、心理言語学とか、計算言語学、計算心理言語学、認知科学とか言われる分野の研究をみていると（これらの分野がそれぞれどういった範囲を指しているのか正直よくわからないが）、確率や情報理論であふれています。 昨年、2024年夏にオランダのロッテルダムであった CogSci（認知科学の国際会議）に参加したら、これが私にとって初めての海外での国際会議だったわけですが、何とまあ端から端まで情報理論かベイジアンモデリングで割と衝撃を受けました。 そういった状況が良いか置いておいて、とりあえず勉強しなきゃなぁと思わされたし、この波に乗っておきたい、と思えました。ので、その紹介記事です。

このあたりのレビュー論文、本として、個人的参照すべきものたち：

目次

文処理系

Surprisal

ある単語 $w$ の生起確率 $P(w)$ の 負の対数 $-\log P(w)$ のことを単語 $w$ のサプライザルと呼びます。 サプライザル理論 (Hale, 2001; Levy, 2008b) では、ある単語の予測のしにくさ（サプライザル）はその単語の処理の難しさに比例する、とします： \begin{equation} \text{difficulty}(w)\propto -\log P(w) \end{equation}

  • 確率値を表すときは大文字 $P$、確率分布を表すときは小文字 $p$ を使うようです。
  • 対数の底はしばしば $2$ で bit単位ですが、底が一致している限りはサプライザル同士の相対関係は変わらないので、底の値自体をサプライザルの定義に組み込む必要は（たぶん）ないです。
    • $\log_2 x = \frac{\log_e x}{\log_e 2} = \frac{\log_e x}{0.30103…}$ と、底の変更は可能。

サプライザルの値 $-\log P(\cdot)$ は、生起確率 $P(\cdot)$ の値が小さければ小さいほどほど大きくなる、という関係になっています。

png

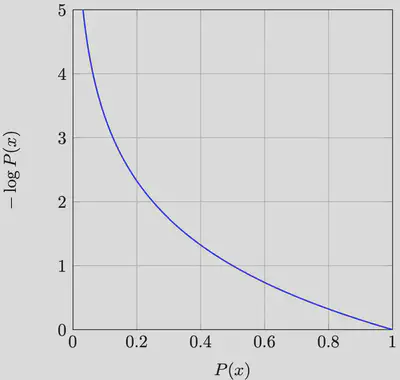
そして、実際に、読み時間 (e.g., Demberg and Keller, 2008; Smith and Levy, 2013; Wilcox et al., 2023; Shain et al., 2024) や、ERP（事象関連電位）(e.g., Frank et al., 2015; Brennan and Hale, 2019)、 fMRIによるBOLD信号 (e.g., Lopopolo et al., 2017; Shain et al., 2020) について、サプライザルが predictor として有効であることが示されています。

サプライザルがとらえているものは何なのか？

では、単語 $w$ の生起確率 $P(w)$ は何で求めることができるのでしょうか。 逐次的な文処理過程について考える場合、単語 $w$ 以前の文脈 $w_1,\dots,w_{n-1}$ が与えられたときの単語 $w$ の生起確率 $P(w\mid w_1,\dots,w_{n-1})$ が求められれば良い、すなわち、言語モデルがあれば良い、ということになります。

Hale (2001) では、言語モデルとして、確率的文脈自由文法（Probabilistic Context-Free Grammar, PCFG）によるものを採用しました。 PCFGは、文脈自由文法における各文法規則に生起確率を割り当てたものです。詳しくは、自然言語処理系においてとりあえず最初に参照すべき文献である Jurafsky and Martin (2025, Appendix C) を参照ください。

$P(w_n\mid w_1,\dots,w_{n-1})$ は、条件付き確率の定義により、 \begin{equation} P(w_n\mid w_1,\dots,w_{n-1}) = \frac{P(w_1 \cdots w_{n-1}, w_n)}{P(w_1 \cdots w_{n-1})} \end{equation} と分解することができます。

PCFGは、文脈自由性により、ある文字列に対する可能なすべての木構造は互いに排反なので、以下が成り立ちます： \begin{equation} P(w_1 \cdots w_n) = \sum_{T\in\mathcal{T}(w_1 \cdots w_n)} P(T, w_1 \cdots w_n) \end{equation}

また、PCFGは木構造と文字列の生成モデルであり、木構造 $T$ に対して文字列 $w_1\cdots w_n$ が一意に定まるので、 \begin{equation} P(w_1 \cdots w_n\mid T) = 1 \end{equation} が成り立ちます。

よって、ある文字列 $w_1\cdots w_n$ の確率は、その文字列に対するすべての可能な木構造の確率の和に等しくなります： \begin{align} P(w_1 \cdots w_n) &= \sum_{T\in\mathcal{T}(w_1 \cdots w_n)} P(T, w_1 \cdots w_n) \newline &= \sum_{T\in\mathcal{T}(w_1 \cdots w_n)} P(T)\cdot P(w_1 \cdots w_n\mid T) \newline &= \sum_{T\in\mathcal{T}(w_1 \cdots w_n)} P(T) \end{align}

つまり、サプライザル $-\log P(w_n\mid w_1,\dots,w_{n-1})$ は、 \begin{align} -\log P(w_n\mid w_1,\dots,w_{n-1}) &= -\log\frac{P(w_1 \cdots w_{n-1}, w_n)}{P(w_1 \cdots w_{n-1})} \newline &= -\log\sum P(n\text{単語までの木構造}) \newline &\quad - \log\sum P(n-1\text{単語までの木構造}) \end{align} と、$n$ 単語時点での構造に関する情報量と $n-1$ 時点での構造に関する情報量の差、言い換えると、その単語により構造に関してどれだけ情報が得られたのか、を表す値として説明されます（解説として、Hale (2016) も参照ください）。

Hale (2001) でPCFGが採用されたのは、$n$-gram 言語モデルでは（$n$ がとりわけ大きいわけではなければ）単語間の依存関係を正しく取り扱えないからであり、さらにはそもそも著者自身の興味が文法構造の処理にあったからだと思われるのですが、それにより、シンボリックで離散的な文法理論を、連続的で柔軟な情報理論を通して、処理負荷の予測につなげられています。

* そのため、Hale (2006) では、PCFG ではなく、linguistically-motivated な Minimalist Grammar を用いてモデリングを行っています。構造への確率が付与できさえすれば良いので、そういった拡張が容易にできます。

これに対し、Levy (2008b) では、特定の構造・意味の形を前提としない形でのサプライザルの解釈を提示しました。

アイディアは非常にシンプルで、$n$ 時点での単語 $w_n$ のサプライザルを、　$n-1$ 時点までの意味 $T\in\mathcal{T}$ の確率分布から $n$ 時点での意味の確率分布へのKL距離（Kullback–Leibler divergence）、すなわち、単語 $w_n$ の入力により、意味に関する確率分布がどれだけ変化するのかを示す値である、と示しました。 これは、先ほどの Hale (2001) でのサプライザルの導出過程と同じで、$P(w_1,\cdots,w_n\mid T) = 1$ 、という仮定を置いた場合に示すことができます： \begin{align} &D_{\textit{KL}}(p(T\mid w_1\cdots w_{n})\parallel p(T\mid w_1\cdots w_{n-1})) \newline &= \sum_{T\in\mathcal{T}} p(T, w_1\cdots w_n)\log\frac{p(T\mid w_1\cdots w_n)}{p(T\mid w_1\cdots w_{n-1})} \newline &= \sum_{T\in\mathcal{T}} p(T, w_1\cdots w_n)\log\frac{\frac{p(w_n\mid T, w_1\cdots w_{n-1})p(T\mid w_1\cdots w_{n-1})}{p(w_n\mid w_1\cdots w_{n-1})}}{p(T\mid w_1\cdots w_{n-1})} \newline &= \sum_{T\in\mathcal{T}} p(T, w_1\cdots w_n)\log\frac{\frac{p(T\mid w_1\cdots w_{n-1})}{p(w_n\mid w_1\cdots w_{n-1})}}{p(T\mid w_1\cdots w_{n-1})} \newline &= \sum_{T\in\mathcal{T}} p(T, w_1\cdots w_n)\log\frac{1}{p(w_n\mid w_1\cdots w_{n-1})} \newline &= \log\frac{1}{p(w_n\mid w_1\cdots w_{n-1})} \newline &= -\log p(w_n\mid w_1\cdots w_{n-1}) \end{align}

言語モデルが妥当に単語の確率分布を推定できるのならば、その言語モデルが計算するサプライザルは、背後の意味・構造に関する分布を考慮に入れられているよ、ということが示されているのは非常に面白いところです。

しかしながら、ではなぜ現在の大規模言語モデルによるサプライザルが人間の読み時間・神経活動を（かなり説明はできているが）説明しきれていないのでしょうか。 おそらくは、人間の作業記憶は大きくない、という制約や、確率分布等の計算をすること自体のコストが考慮されていないからでしょう。 Hale (2001) では $T$ で周辺化された文字列に関する周辺分布を、Levy (2008b) では、$T$ に関する確率分布を用いてサプライザルを説明していますが、人間が、こういった分布を全部ちゃんと記憶して扱えるのかは謎です。おそらく絶対に分布を端から端までは記憶していないでしょう。次に調べるべきところは、分布を想定するという理想化により現実とどのくらい差異が生じうるのか、ということでしょう。 また、（これは些細であるのかどうかの判断もついていないのですが）$P(w_{1,\cdots,n}\mid T)=1$ という仮定は問題ないのでしょうか。真理条件的には同じ意味だが、語順・構造が違う文は作れるし、語彙も「同じ意味っぽい」形が異なる組み合わせはたくさんあるが、とは思います。

言語モデルの性能 (perplexity) との関係

言語モデルの次単語予測性能を表す（単語ごとの）perplexityは、その値が低いほど「テストデータにおける次単語予測が正確である」ことを表すのですが、一時期は、「言語モデルのperplexityが低いほど、そのモデルによって算出したサプライザルの、読み時間の予測精度が高い」ということが主張されていました (Goodkind and Bicknell, 2018)。 しかし、次第に、Oh and Schuler (2023) や Shain et al. (2024) など、「言語モデルの規模が大きくなり、perplexityがさらに低くなっていくと、むしろ読み時間予測精度が下がる」という傾向が観察されているようです。 確かに、人間以上に次単語予測ができるモデルは、人間の反応時間をunderestimateしてしまうでしょう。とはいっても、大規模言語モデルのサプライザルは人間の反応についてかなりの程度説明できているのは確かです。

* 言語モデル $q$ のperplexityとは、 \begin{equation} b^{-\frac{1}{|\text{test data}|}\sum_{\text{test data}}\log_b q(x)} \end{equation} で、要は $b$ のテストデータにおける平均サプライザル（クロスエントロピー）乗です。$b$ は底 (base) で、一貫していればなんでもいいです。

サプライザルと処理負荷の関係は線形か、非線形か

hoge

Lossy-context surprisal

前項でのサプライザルの定義では、それまでの文脈をフルに使って求められた当該単語の生起確率が用いられていました。 一方で、心理言語学の文処理研究では、昔から、人間は作業記憶に極めて制限があり、記憶にまつわる処理の負荷があることが知られていました。 この予測に関する処理負荷と記憶に関する処理負荷は、要は文処理に関する2大処理負荷で、ずっと別々に研究が進んでいたのですが、Futrell et al. (2020) では、サプライザルの定義を少しだけ変更した lossy-context surprisal (LCS) を提案し、この2つを統合しました（これはほんとうにすごいと思っています）。 アイディアはものすごいシンプルで、文脈 $c = w_{1,\cdots, n-1}$ をフルに使用せず、文脈 $c$ をもとにした記憶表象 $m$ を用いて、単語 $w$ の生起確率を求める、というものです： \begin{align} \text{LCS}(w\mid c) &:= \mathbb{E}_{m\sim p(m\mid c)} [-\log p(w\mid m)] \newline &= -\sum_m p(m\mid c)\log p(w\mid m) \end{align}

この定式化は非常に一般的なものであり、例えば記憶表象 $m$ がどのような形なのか、どのようにして生成されるのか、といったことは特に指定されていません。 ということは、この形を明らかにする、という研究は求められるはずで、例えば 単純に文字列としての $c$ と $m$ の関係なのかもしれないし、意味（構造）として $m$ を扱った方が実際の人間がやっていることに近いのかもしれません。 記憶に関する処理については、これまで、Gibson (1998) や Lewis and Vasishth (2005)、Isono (2024) など、何らかの文法理論を用いてモデル化がなされてきており、人間の記憶単位（チャンク）は文法構造を考えると良さそうかも、という状況です。 なので、これらを組み合わせることはできるし、そして人間の文処理のモデル化として有効でしょう、ということは期待できます。 一方で、「こうしたモデル化をしないと説明できないこと」みたいなものを私は思いついていないので、特にやるモチベーションはまだないです。 少なくとも、Hale (2001) や Levy (2008b) が考えていたような定式化において、分布全体を把握できているのは理想化のしすぎに思えるので、それが少し緩和される、というのは良いことかもしれません。

Noisy-channel model

人間の文処理研究において、多くの場合、人間は見聞きした文を正確に知覚できていることが前提とされていたりしますが、もちろん常にそんなことはなく、実際には聞き手は、話し手の発話を一部聞き逃したり、誤って聞き取っている場合もあります。 しかしながら、だからといって聞き逃して終わり、というわけではなく、聞き手は何やかんやうまく話し手の意図を推定できたりしています。 このような人間の処理過程を、Levy (2008a) や Gibson et al. (2013) は、noisy-channel model（雑音のある通信路モデル）を用いてモデル化しました。

ここでは簡単に Gibson et al. (2013) による表記を用いて紹介します。 \begin{equation} s_i \overbrace{\longrightarrow}^{\text{noisy channel}} s_p \end{equation} 話し手が意図した発話 $s_i$ が、聞き手が実際に知覚した発話 $s_p$ をもとに推定される確率 $P(s_i\mid s_p)$ は、 \begin{equation} P(s_i\mid s_p)=\frac{P(s_p\mid s_i)P(s_i)}{\sum_{s_j\in\mathcal{S}}P(s_p\mid s_j)P(s_j)}\propto P(s_p\mid s_i)P(s_i) \end{equation} で求められます。

ようは、$P(s_p\mid s_i)$ という noise が入る確率と、そもそもありえる発話 $s_i$ の確率 $P(s_i)$ のバランスをとって、 $s_i$ を合理的に推定する、ということです。 Gibson et al. (2013) の例を使うと、The mother gave the candle the daughter. という文は、the candle に the daughter を与えたという意味的に不自然な文（つまり、$P(s_p)$ は低い）が、名詞同士の間に to を入れ忘れた可能性は高そう（$s_i$ が The mother gave the candle to the daughter. と考えたとき、$P(s_p\mid s_i)$ の確率は高そう）なので、おそらく多くの人は、文字通りではない意味 The mother gave the candle to the daughter. で解釈しそう。 一方で、The girl was kicked by the ball. は、意味的に不自然で $P(s_p)$ の確率は低そうなのだが、他の意味的に妥当な文を探してきても、$P(s_p\mid s_i)$ が $P(s_p)$ を超えることはあまりなさそう（これは事前確率と尤度をどう計算するか次第ではあるが）なので、文字通りの解釈が取られやすい、と考えられます。

Ferreira and Ferreira (2024) では、noisy-channel model が good-enough model に似ている、と説明していますが、むしろ noisy-channel model はちゃんと予測がたつ理論、という意味ではより強力なものだとは思います。

個人的には、Competence $c$ とPerformance $p$ の間の関係も、まさにnoisy channelで考えることができる、と思っていています。 \begin{equation} c \overbrace{\longrightarrow}^{P(c\mid p)} p \end{equation}

例えば、$P(c)$ はオッカムの剃刀的な、シンプルな理論ほど高い確率を付与する、というふうにして表現できますし、$P(p\mid c)$ は、competence $c$ によって performance $p$ をどれだけ説明できるのか、ということで、まさに理論言語学者や心理言語学者が、容認性判断や読み時間、神経活動データなどをもとに判断していることでしょう。概念的には、 \begin{equation} P(p) = \sum_c P(p\mid c)P(c) \end{equation} の $P(p)$ と実際の観測との誤差が最小になるような $P(p\mid c)$ を探す、ということをしているはずです。

そして、$P(p\mid c)$ や $P(c)$ を定めることができれば、$P(c\mid p)$ が推測できます： \begin{equation} P(c\mid p)=\frac{P(p\mid c)P(c)}{\sum_{c\in\mathcal{C}}P(p\mid c)P(c)}\propto \underbrace{P(p\mid c)}_{\text{現象への説明}}\overbrace{P(c)}^{\text{文法のシンプルさ}} \end{equation}

つまり、$P(c\mid p)$ は、competence自体の単純さとそれによる説明力の高さのトレードオフにより求められます。 そして、最も適切な理論 $\hat{c}$ は、事後確率が最大となるもの、とすることができます： \begin{equation} \hat{c}=\arg\max_{\hat{c}\in C} P(p\mid c)P(c) \end{equation}

尤度と事前確率をそれぞれ「記述的妥当性」と「説明的妥当性」として読むと、これはまさに Chomsky (1965) による competence-performance の区別における議論でしょう。 記述的妥当性と説明的妥当性のトレードオフは、 Berwick (2015) が最小記述長 (minimum description length) を用いて同様の議論をしています。

ただ、このnoisy-channel model は非常に一般的なことを述べているに過ぎないので、Chomsky による competence-performance をより広く解釈できます。 50-60年代は容認性判断くらいしか $P(p\mid c)$ の議論をする場所がなかったので、Chomsky の議論は文法現象の「記述」がメインでしたが、心理言語学研究の進展により、$P(p\mid c)$ に対して、読み時間や脳活動データを使った検証が可能です。

また、Kirby et al. (2015) での文法の文化進化モデルも、尤度を「意図の伝達成功確率」と、事前確率を「文法の学習可能性」として扱っているもの、と見ることができると思います。

とはいっても、Chomsky の50-60年代の直感は、いまになって読み返してみても、（Shannon の研究を必要以上に叩いているようにみえるところ以外は）非常に有用なものが多いように思えます。 ちゃんと整理すると、$P(c),\ P(p\mid c),\ P(c\mid p)$ それぞれについて考えようとする、ということがまっとうな Chomskian だと思っているのですが、どうでしょうか。 そういう意味で、個人的には、formal な文法理論を用いた文処理の研究 ($P(p\mid c)$) と、$P(c\mid p)$ に直接取り組む効率的なコミュニケーション研究（後述）をやっています。学習可能性 ($P(c)$) に関する研究もしてみたいとは思っています。

* もしくは、$c$ と $p$ の間に noise が入りえない、プロの言語学者ならば noise なしで自身の $c$ にアクセスできる、と考えるのも、それが実現可能かはおいておいて、筋は通っているとは思います。そういう考え方に基づくと、$P(p\mid c)$ なんてものは考える必要はなくなります（では、心理言語学研究は何をやっていることになるのでしょうか）。

効率的なコミュニケーション (Efficient Communication)

確率や情報理論により、言語使用や人間のコミュニケーションにおける cost/benefit を心理的に妥当な指標で評価できるようになってきました。 また、計算機上では、「現実には存在しないがありえたかもしれない仮想的な言語」を作り出すことができるので、言語に見られる構造・規則が言語使用において明らかに有利なものであるのか、といったことを検証することが可能です。

効率的なコミュニケーション仮説 (Efficient Communication Hypothesis) では、言語構造が効率的なコミュニケーションを実現するように形作られてきた、と考え、言語に存在する普遍性 (universalities) や 強い統計的傾向 (strong statistical tendencies) がなぜあるのか、ということを言語使用に帰して説明しようとしています。

おすすめレビュー論文、本：

  • Jaeger and Tily (2011)
    • 心理言語学研究からはじめて typology にまで話を広げましょう、というレビュー論文
  • Kemp et al. (2018)
    • 特に lexicon (semantic categorization) に関する研究を牽引してきた著者たちによる Annual Review of Linguistics のレビュー論文
  • Gibson et al. (2019)
    • 心理言語学の立場から、単語の長さや色の語彙、語順について処理の効率性の観点で説明してきた著者らによるレビュー論文。
  • Futrell and Hahn (2022)
    • Gibson et al. (2019) に加え、さらに情報理論それ自体の説明やその応用について解説しているレビュー論文。
  • Levshina (2022)
    • 個別具体的な言語現象にそれぞれ注目して言語の効率性について論じた本。

* なお、ここでの「コミュニケーション」とは、文化・社会的要因等を考慮したり、ジェスチャーなどの非言語的情報を考慮する、といったようなレベルにまではまだ達しておらず、より単純に単語や句、文の伝達を指します。 言語学や心理学、認知科学で扱われてきた、文レベルを超えたコミュニケーションについては、まだまだこれからです。

単純性と情報伝達性のトレードオフ

コミュニケーションが効率的であるとは、人間の認知能力の制約のもと、「意図・情報の伝達が最大化されている一方、産出や理解といった使用のコストが最小化されている状況」のことを指す、という表現を私は使います。 つまり、できる限り informative でありかつできる限り simple である状況が効率的であります。

この情報伝達性 (informativeness) と単純性 (simplicity) にはトレードオフ関係があり、つまり、どちらか一方だけを高めるともう一方は低くなってしまう、という関係であり、自然言語は、このトレードオフのもとで（ほとんど）最適解である側面が数々観察されています。

「最適解」とは、お気持ちレベルの説明すると、「片方の軸における値をより良い方に持っていくと、どうしてももう片方の軸における値が悪い方に行ってしまう点」のことを指します。 そういった点は1つに定まるわけではなく、下の図のように曲線を描くはずです。 この最適解のことをパレート解と、そしてパレート解を結んでできる曲線のことをパレートフロンティアといいます。

png

* 『自然言語処理』の学会記事 (to appear) でも書いたのですが、simplicity と informativeness という用語は専門用語として固まってきてしまっているようなのですが、その意味するところが伝わりにくい表現であります。 私自身は informative という単語の語感がそもそもわからないので何とも言い難いですが、そもそも「コミュニケーションの効率性」をどういった概念・シナリオで考えるのか、そしてそれをどういった表現で言い表すのか、といったことの整理は、今後時間をかけてなされていくものなのでしょうかね。トレードオフの概念をもっとも抽象的に（それゆえに正確に？）表すとすると、complexity/accuracy とかでしょうか。それか、cost/benefit とか、cost/reward とかでしょうか。そして、こうした抽象的な概念を、人間の言語処理の問題として表現するとなると、Piantadosi et al. (2012) で使われていた、ease/clarity がいいですよね。とは思っています。

2つの相反する圧力のもとでの最適化、として言語を説明する研究は、Zipf (1949) や Hawkins (1994)、Haspelmath (2008) など、言語学者の間でも主張されてきたものですが、効率的なコミュニケーション研究は、それを理論中立的な情報理論のことばを使って書き下すことにより、定量的な研究を実現するだけでなく、その適用先・規模を拡大させることができた、という点が大きな進展だったのだと思っています。 特に語彙 (wordformやsemantic categorization) や、最近では文レベルについても研究が進んできています：

語彙に関して：

文法に関して：

効率的なコミュニケーション研究について、実際に情報理論の道具を使ってどう仮説を検証するか、代表的な研究を紹介しながら説明します。

Ferrer i Cancho and Sole (2003)

Ferrer i Cancho and Sole (2003) では、世界中の言語に見られるZipf則 (Zipf’s law) (Zipf, 1936; 1949) が、効率的なコミュニケーションの実現の結果として生まれるものなのかを検証するため、コミュニケーションを効率的にしたときにZipf則が立ち現れるのかシミュレーション実験をしました。 この研究は、効率的なコミュニケーション研究の先駆けであるので紹介します。

まず、前提として、Zipf則とは、単語頻度に関する経験則で、全体で$k$番目に多く使用される単語の頻度 $f(k)$ は、$f(k)=C\cdot k^{-\alpha}$ と冪乗則に従う、というものです。要は、よく使われる単語はめちゃくちゃ使われるし、珍しい単語は本当に珍しい、というものです。 $C$ は比例定数で、$\alpha$ は Zipf (1949) では $1$ です。 両辺に対数を適用すると、$\log f(k) = -\alpha\log k + \log C$ と線形な関係になります。

実際の頻度と頻度ランクの関係を見たら、式の意味はすぐにわかります。 ちょうど手元にUD_Japanese-BCCWJのv2.10、国語研長単位 (LUW) 分割があったので、これの単語頻度と頻度ランクを数えてみました。 全部で57,109文、995,632単語（長単位）で、x軸を頻度ランク、y軸を実際の頻度としてプロットしたのが左図、そして両軸に $\log_{10}$ を適用してプロットしたものが右図です。

png

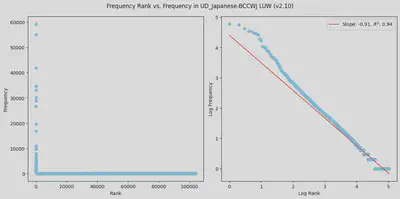
右図については、最小二乗法での回帰直線も引いてみました。 $\alpha = 1$ とはなっていないようですが、ある程度はZipf則に従っているようにみえます。

* 直線から逸脱している部分があることや、傾きの係数が $0.94$ であることを「Zipf則に従っている」とみるか、は結構重要な問題な気はします。 詳しくは Piantadosi (2014) をお読みください。

では、（一旦単語分布はZipf則に従っているとして）なぜ単語分布はZipf則に従うのでしょうか。 Zipf (1949) は、言語は、省エネでありたいという話し手の要求と、意図・情報の復元が容易でありたいという聞き手の要求のトレードオフのもとで形作られているのだという仮説を提案しました。 具体例として、言語を「単語」と「意味」の対応関係と考えてみましょう。 すべての意味をたった一つの単語で表現する言語があったら、話し手は覚えるべき単語が一つだけになるため、話者の負担は最小限になります。 しかし、このような言語では、単語がどの意味を指すのか曖昧になり、聞き手が話者の意図を理解するのに困難が生じます。 一方で、すべての単語が明確に異なる意味を表現するシステムでは、聞き手の理解（意図推定）は容易になりますが、話し手の負担は増加します。 Zipf は、言語はこうした話し手と聞き手の相反する要求のバランスによって形作られているのだと主張しました。

では、それは本当か？と計算機上で実験してみたのが、Ferrer i Cancho氏 と Sole氏 の研究です。

モデル

彼らは、上述した Zipf の説明を検証するため、信号（単語）と意味の対応関係について、話し手と聞き手双方のコストがトレードオフのもとで最小となるような関係になるまで進化アルゴリズムを使って推定する、ということを行いました。

$n$ 個のシグナル $\mathcal{S} = {s_1,…,s_i,…,s_n}$ と $m$ 個の意味（objects of reference）$\mathcal{R} = {r_1,…,r_i,…,r_m}$ を考えたとき、それらの間の関係をバイナリ行列 $\mathbf{A} = {a_{ij}}\ (1\leq i\leq n,\ 1\leq j\leq m)$ で表します。

バイナリ行列は、すべて $0$ か $1$ で構成されている行列で、ここでは、ある $i$ 番目のシグナル $s_i$ が $j$ 番目の意味 $r_j$ を表している場合、行列内の要素 $a_{ij}$ は $1$ と、そうでないならば $0$ と表現します。

いま、synonym（同義語）があるなら、シグナルと意味の確率分布の関係は以下になります： \begin{equation} P(s_i) = \sum_j P(s_i,r_j) \end{equation}

なお、$P(r_i) = 1/m$ と仮定。

ベイズの定理より、 \begin{equation} P(s_i,r_j) = P(r_j)P(s_i\mid r_j) \end{equation} であり、$P(s_i\mid r_j)$ は、 \begin{equation} P(s_i\mid r_j) = a_{ij}\frac{1}{\omega_j}. \end{equation} で定義します。 $\omega_i = \sum_j a_{ij}$ は意味 $r_j$ における同義語の数です。

代入すると、 \begin{equation} P(s_i,r_j) = a_{ij}\frac{P(r_j)}{\omega_j} \end{equation}

話し手と聞き手のコストは、それぞれ平均情報量（エントロピー）で定義します： \begin{align} H(S) &= -\sum_i^n P(s_i)\log P(s_i) \newline H(R\mid S) &= -\sum_i^n\sum_j^m P(s_i,r_j)\log P(r_j\mid s_i) \end{align}

そして最後に、話し手と聞き手のコストのトレードオフは、それぞれの加重和で表現します： \begin{equation} \Omega(\lambda)=\lambda H(S) + (1-\lambda)H(R\mid S) \end{equation} ここで、$0\leq\lambda\leq 1$ で、話し手と聞き手のコストのどちらを重視するかを表します。

この $\lambda$ の値を変えながら、各 $\lambda$ において、$\Omega(\lambda)$ を最小化するようなバイナリ行列 $\mathbf{A}$ を進化アルゴリズムで求める、ということをします。

再現コードと結果

非常に単純なモデルなので、再現実装してみました（いくつか簡略化しています）。

png
png
png

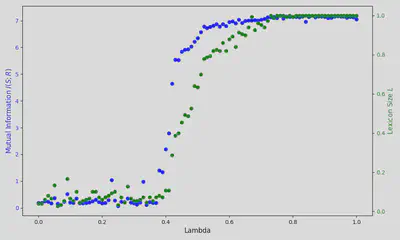
最適化の結果として、$\lambda = 0.41$ あたりで、Zipf則に近い分布が得られることがわかりました。

もちろん、目的関数が心理的に妥当ではないという批判はあります (Piantadosi; 2014)。 具体的には、通信コードとしての複雑さ（＝エントロピー）が、人間の発話にとっての複雑さと一致しているのかは誰も示していない、ということと、すべての意味が等確率で現れるという前提は明らかに現実に則していない、ということです。 後者については、Ferrer i Cancho (2005) で提案されているように、意味の分布が一定ではない、と想定した上で、条件付きエントロピー $H(R\mid S)$ を負の相互情報量 $-I(S; R)$ に置き換えると少しは良くなるかもしれません。

負の相互情報量は、 \begin{equation} -I(S; R) = H(R\mid S) - H(R) \end{equation} であり、これまでの式は $H(R)$ が定数であることを想定したものだった、と考えられます。

Zaslavsky et al. (2018)

コミュニケーションにおける最適解を求めるのに、Ferrer i Cancho and Sole (2003) のように進化アルゴリズムのような探索的な方法をとる、ということ以外に、Zaslavsky et al. (2018) は、情報ボトルネック (information bottleneck) を用いて理論的な限界を求める、という方法論を提案しました。

形や意味の確率分布さえちゃんと定められれば、使える方法なので、極めて強力です（特に語彙レベルだと、形と意味の集合を合理的に想定することができるので非常に有用です。文レベルだと、集合や分布を決める、というのにおいてまだ良い方法論が見つけられていない気がします）。

hoge

Rational Speech Act (RSA)

Rational Speech Act (RSA) モデル (Frank and Goodman, 2012) は、その名の通り、「話し手の合理的な発話」をモデル化したモデルです。 話し手が合理的であるとは、「話し手は、必ずしも全部を言ってくれるわけではないが（parsimoniousであるが）、何らかの意図を伝えようとできる限りinformativeな発話をする」ということです。

こうした状況はGrice以来想定されてきたわけですが、RSAではその話し手の合理性を確率変数に対するutility関数の形で表現し、聞き手の語用論的推論 (pragmatic reasoning) はベイズ推定 (Beyesian inference) で定式化しました。

話者の合理性を表すutility関数は、さまざまな亜種はあるものの、多くの場合、聞き手にとってinformativeである一方、自分にとってコストが低い発話、という、informativenessとaccessibility (cost) のトレードオフを表現したものが使われます。

具体的には、意味 $m\in\mathcal{M}$ と発話 $u\in\mathcal{U}$ について、utility関数 $U(m,u)$ は、 \begin{equation} U(m,u) = \log P_L(m\mid u) - C(u), \end{equation} ここで、$\log P_L(m\mid u)$ は聞き手にとってのinformativeさを、$C(u)\geq 0$ は発話それ自体のコストを表します。

そして、実際の話し手の発話の確率は、このutility関数の値をもとに確率的に決まると考えると、ソフトマックス関数を通して求めることができます： \begin{equation} P_{S_t}(u\mid m) = \frac{e^{\alpha U_{t-1}(u,m)}}{\sum e^{\alpha U_{t-1}(u,m)}} \propto e^{\alpha U_{t-1}(u,m)}, \end{equation} ここで、$\alpha$ は話し手がutilityにどれだけ重みを置いているかを表します。

こうして話し手の合理的な発話がモデル化できると、聞き手の語用論的推論は、ベイズ推論によって表現することができます： \begin{equation} P_{L_t}(m\mid u) \propto P_{S_t}(u\mid m)P(m) \end{equation}

なお、添え字の $t$ や $t-1$ は、合理的な話し手が再帰的な思考の内部で想定した、話し手および聞き手モデルの埋め込みのレベルを指します。 要は、合理的な話し手は、「合理的な話し手ならこう言うだろう、ということを合理的な聞き手は推定するんだろうな、だからこういおうかな…」という推論を再帰的に繰り返し続けることができ、毎度ひとつ前の埋め込みでの聞き手を想定したうえで発話選択をする、ということを繰り返している、ということです。

ただし、もちろん、この再帰的な話し手と聞き手の関係は無限に考えることができるが、それだと推論がいつまでたっても終わらないので、通常は、1回埋め込んだところに、“literal listener” $P_{Lit}$ を想定します。

literal listner は、語用論的推論は行わず、文字通り、意味の真偽を判断します： \begin{equation} P_{Lit}(m\mid u) \propto \delta_{[[u]]}(m) P(m), \end{equation} ここで、$\delta_{[[u]]}(\cdot)$ は、真偽値の $0, 1$ を返す関数です。 これにより、RSA frameworkにlexical semanticsやcompositional semanticsを組み込むこともできる、という主張です。

もう一度流れを整理すると（埋め込みが1回の場合）、 $t$ における合理的な話し手の発話は、 \begin{equation} U(m,u) = \log P_{L_{t-1}}(m\mid u) - C(u) \end{equation} というutility関数をもとに、 \begin{equation} P_{S_t}(u\mid m) \propto e^{\alpha U_{t-1}(u,m)} \end{equation} でモデル化することができます。 ここで、utility関数内の $P_{L_{t-1}}$ をliteral listnerと考えると、 \begin{equation} P_{Lit}(m\mid u) \propto \delta_{[[u]]}(m) P(m) \end{equation} で $P_{L_{t-1}}$ をモデル化できます。

そうして、$t$ における聞き手の語用論的推論は、 \begin{equation} P_{L_t}(m\mid u) \propto P_{S_t}(u\mid m)P(m) \end{equation} で求めることができます。

RSA 関連でとりあえず参照すべきもの：

Uniform Information Density (UID)

hoge

Dependency Length Minimization (DLM)

hoge

Memory–prediction trade-off

hoge

言語獲得

確率モデル、というかベイズの定理を利用した言語学・認知科学研究で忘れてはならないのが、言語獲得のモデル化です（ベイジアンモデリングの解説については、Griffiths et al. (2010) や Griffiths (2024) へ）。

\begin{equation} P(h_i\mid d)=\frac{P(d\mid h_i)P(h_i)}{\sum_{h_j\in\mathcal{H}}P(d\mid h_j)P(h_j)}\propto P(d\mid h_i)P(h_i) \end{equation}

世の中にはベイズの定理に関する解説で満ち満ちているので適当に書きますが、簡単に説明すると、上式は、データ $d$ を受けたとき、仮説 $h_i\in\mathcal{H}$ をどれだけ支持するか、という確率 $P(h_i\mid d)$ は、その仮説 $h_i$ の事前確率 $P(h_i)$ と、その仮説 $h_i$ をもっていたときにデータ $d$ に出会う尤度（尤もらしさ）$P(d\mid h_i)$ の積でわかりますよ、ということです。

ベイズの定理の嬉しさは、概念上は、生得主義 vs. 経験主義といった二項対立を超えて、言語はどのくらい学習可能か、どのくらいの生得知識 (inductive bias) が必要か、ということを定量的に評価することができるはず、というところでしょう、と、私は思っています。 これについて、Chater and Manning (2006) で説明があるので、引用して紹介します。

以下、Chater and Manning (2006) の p.342より：

Oversimplifying somewhat, suppose that a learner wonders whether to include constraint $C$ in her grammar. $C$ happens, perhaps coincidentally, to fit all the data so far encountered. If the learner does not assume $C$, the probability that each sentence will happen to fit $C$ by chance is $p$. Thus, each sentence obeying $C$ is $1/p$ times more probable, if the constraint is true than if it is not (if we simply rescale the probability of all sentences obeying the constraint). Thus, after $n$ sentences, the probability of the corpus, is $1/p^n$ greater, if the constraint is included. Yet, a more complex grammar will typically have a lower prior probability. If the ratio of priors for grammars with/without the constraint is greater than $1/p^n$, then, by Bayes’ theorem, the constraint is unlearnable in $n$ items.

ようは、ある制約 $C$ が生得知識としてあるべきなのか、それとも学習可能なのかは、制約 $C$ がある文法（仮に $G_C$）と制約 $C$ がない文法（仮に $G_{\neg C}$）の事前確率の比 $\frac{P(G_C)}{P(G_{\neg C})}$ と尤度比 $\frac{P(d\mid G_C)}{P(d\mid G_{\neg C})}$ を比べることで、事後分布の比 $\frac{P(G_C\mid d)}{P(G_{\neg C}\mid d)}$ を比べるのと同じこととなり、制約 $C$ が学習可能なのかを判定することができる、ということです。

仮に、$G_{\neg C}$ を想定している人が、偶然にも $G_{C}$ に整合的な文 $s_C$ に出会う確率を $p$ とすると、$P(s_C\mid G_{\neg C}) = p$ です。 $P(s_C\mid G_{C}) = 1$ であるとすると、ある人が $G_{C}$ に整合的な文に $n$ 回出会ったとき、それぞれの文法を想定したときの尤度比は、$\frac{P(s_C\mid G_{C})^n}{P(s_C\mid G_{\neg C})^n} = \frac{1}{p^n}$ です。 このとき、それぞれの文法の事前確率 $P(G_C)$ と $P(G_{\neg C})$ の比が $\frac{1}{p^n}$ 分離れているのかどうかで、制約 $C$ が学習可能なのかどうか決まります。 基本的には、制約が一つ多い文法の方が複雑で事前確率がより小さくなっているはずだが、その小さい事前確率をもってもなお尤度により挽回可能なのか、ということです。

Xu and Tenenbaum (2007)

hoge

Perfors et al. (2011)

hoge

Abend et al. (2017)

hoge

Yang and Piantadosi (2022)

hoge

言語進化

繰り返し学習モデル (Iterated Learning Model)

hoge

Kohei Kajikawa
Kohei Kajikawa
PhD student at NINJAL.

My research interests include computational linguistics and computational psycholinguistics.