CCGについて
Published:
CCG(Combinatory Categorial Grammar; 組合せ範疇文法)に関する文献案内・parser案内など。
2分でわかるCCG
- 各単語・句には category(範疇)が割り当てられる。
- Category には atomic なものと complex なものがある。
- Complex category は、category と 2種類の slash ( \( / \), \( \backslash \) ) で構成される。
- \( X/Y \) は、\( Y \) を右側にとったら \( X \) になるもの。
- \( X\backslash Y \) は、 \( Y \) を左側にとったら \( X \) になるもの。
- slash の右側 ( \( Y \) ) が項、左側 ( \( X \) ) がその項をとった結果。
- slash の向きが、項をとる位置を指定する。
- 形式的に書くと、category の集合を \( \mathcal{C} \) としたとき、
- \( \mathcal{A}\subseteq\mathcal{C} \) となる atomic category の集合 \( \mathcal{A} \) がある
- 任意の category \( X, Y\in\mathcal{C} \) について、 \( X/Y, X\backslash Y\in\mathcal{C} \)
- 例えば、atomic なものとして NP(名詞句) と S(文) を想定すると、英語の自動詞は、S\NP。他動詞は (S\NP)/NP。
- He ran の ran は、左側に NP をとったら S になるので、S\NP。
- He ran a hotel の ran は、右側に NP を、そしてさらに左側に NP をとったら S になるので、(S\NP)/NP。
- slash は left-associative(左側結合)なので、\( X/Y/Z \) と \( (X/Y)/Z \) は同じ。
- Category には atomic なものと complex なものがある。
- 各 category に再帰的に combinatory rule(組合せ規則)を適用し、統語構造を構成する。
- Function Application(関数適用): \begin{array}{lll} \mathit{X/Y} \quad \mathit{Y} & \Longrightarrow_{>} & \mathit{X} \newline \mathit{Y} \quad\;\; \mathit{X\backslash Y} & \Longrightarrow_{<} & \mathit{X} \end{array}
- Function Composition(関数合成): \begin{array}{lll} \mathit{X/Y} \quad \mathit{Y/Z} & \Longrightarrow_{>\mathbf{B}} & \mathit{X/Z} \newline \mathit{Y\backslash Z} \quad \mathit{X\backslash Y} & \Longrightarrow_{<\mathbf{B}} & \mathit{X\backslash Z} \end{array}
- Type Raising(型繰り上げ): \begin{array}{lll} \mathit{X} & \Longrightarrow_{>\mathbf{T}} & \mathit{T/(T\backslash X)} \newline \mathit{X} & \Longrightarrow_{<\mathbf{T}} & \mathit{T\backslash (T/X)} \end{array}
- 代表的な combinatory rule は、上記の3つ。
- \( \Longrightarrow \) の左側のものが右側のものになる、ということを表している。
- \( \Longrightarrow \) の右下の記号が、その rule を表す。
- \( \mathbf{B} \) や \( \mathbf{T} \) のようなアルファベットは、コンビネータ論理のコンビネータ由来。
- Steedman (1987) 以前は別の記法ですが、Steedman (1991) 以降は現在のものになっています。
- ここでは省略しますが、各 rule には意味計算もついています。そのため、CCGでは、「単語・句に統語 category を割り当てることができる \( \iff \) 意味表示を割り当てることができる」、が成り立ちます。
- 木構造は範疇文法の慣習から、証明図を使って書く。
- バーの上のものが下のものに書き換えられています。
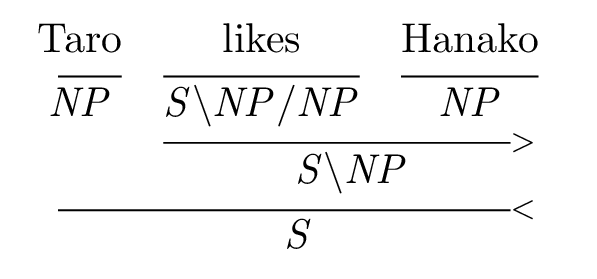
- バーの上のものが下のものに書き換えられています。
文献案内
さらっと雰囲気を掴みたい場合
- Jurafsky and Martin (to appear)
- 自然言語処理の教科書として有名なDan Jurafsky氏とJames Martin氏による Speech and Language Processing のDraftのAppendixの1つ。
- 最低限の組合せ規則と、CCGによるチャートパーザが簡潔に説明されている。
- 言語学の方でも、前半だけ読むと、CCGにどういう文法操作があるのか・どういう構造を作るのか何となく掴みやすいのではないか。
- Steedman (2022)
- Mark Steedman氏による、網羅的なCCGの解説論文。本をギュッと圧縮したイメージ。
- CCG分析で特徴的な構文や関連トピックについて最低限の紙幅で説明されてる。
- 私ははじめ、これと、ここで引用されている文献を行き来して勉強した。
- Clark (2021, arXiv)
- C&C parserのStephen Clark氏によるCCGのparsingに関する論文。
- 後半部分は当時最新のCCG parser作りに関する話だが、前半は、CCGの理論やCCGのparsingの概説・歴史解説として読める。
理論言語学関係
- 統語・意味の理論としてのCCGを理解したい場合に参照すべき文献たちです。
- その他、CCGには音韻の理論としての顔もありますが、そのあたりは詳しくないので含めていません。Steedman (2000) などを参照してください。
- Steedman (1996)
- CCG本の最初。
- LI Monographsで100ページ強。
- CCGで、英語を網羅的に記述できることを示すべく書かれたもの。
- Steedman (2000)
- Steedman (1996) の強化版。
- 若干の理論的改訂あり。
- Google Scholarでは出版年が誤って2001となっており、ちらほら Steedman (2001) として論文中に登場してしまう。
- Baldridge (2002)
- Jason Baldridge氏による博論。
- slash typingを導入し、言語理論としてのCCGを大きく進化させた。
- slash type については、Baldridge and Kruijff (2003; EACL)も参照。
- Steedman (2000) までと違い、等位接続を文法規則 ではなくconjunctのカテゴリ X\X/X で導出。
- 博論なので、解説としても有用。
- 戸次 (2010)
- 日本語CCG本。
- 日本語文法の論文としても面白い。
- 特に活用体系や、量化子周りの話。
- 書評 (矢田部, 2011) も面白い。
- Steedman and Baldridge (2011)
- 非常に簡潔にまとまったCCGの解説論文。
- そのため、Steedman (1996)や(2000)と並んでしばしば引用されている。
- (CCGを引用したいくらいなら、本を読むのは大変なので、こちらを読んで引用した方が良さそう。)
- Non-Transformational Syntaxという本の1チャプター。
- この本はほかの章も良い。Sag and Wasowの章が好き。
- Steedman (2023)
- ほとんどミニマリストに向けて書いてあるLIの論文。
- ミニマリストの理論を踏まえ、「CCGならもっと簡潔に書けますよ」と主張したもの。著者の穏健な姿勢が窺える。
- ミニマリストがCCGをはじめる際には一番わかりやすいと思われる(自分がミニマリストではないのでわからないが)。
- ほとんどミニマリストに向けて書いてあるLIの論文。
- Steedman (to appear)
- Mark Steedman氏によるCCG本のドラフト。
機械の文処理関係
- ここでの機械の文処理とは、文を入力とし、確率的に計算した構文木を返してくれる構文解析器等のことです。
- Clark and Curran (2007; CL)
- C&C parserとして有名。
- CCGbankを使った最初のwide-coverage parser。
- いまだに現役だったりする。Supertaggerの評価用としてよく見る。
- Supertagとは、CCG含め、lexicalized theory of grammarの語彙範疇のこと。
- 通常のPOS tagよりも情報が豊富なので、supertagと呼ばれる。
- 例えば、英語において、動詞原形はPenn TreebankスタイルのPOSだと VB だが、CCGのsupertagだと、S/NP や S\NP/NP などと表す。Supertagの方が、項の数やその相対位置の情報を含む。
- 単語列(=文)に対して、対応するsupertag列が決まれば、ほとんど文の構造は決まるので、supertagging は ‘‘almost parsing’’ であるとも言われている (Bangalore and Joshi, 1999; CL)。
- Hockenmaier and Steedman (2007; CL)
- 英語CCGbank。
- 空白なし小文字b
- Penn Treebank (Wall Street Journal) からの自動変換。
- 英語CCGbank。
- Lewis and Steedman (2014; EMNLP)
- EasyCCG として有名。
- 深層学習 + A* search。
- Uematsu et al. (2013; ACL)
- 日本語CCGBank。
- 空白なし大文字B
- 係り受けコーパスである京都大学テキストコーパス(毎日新聞)からの自動変換。
- 日本語CCGBankの続きとしては、以下のようなものがあります。
- Kubota et al. (2020; LREC) による ABCTreebank
- The Keyaki Treebank からの自動変換
- Tomita et al. (2024; EACL)
- ABCTreebank と lightblue による日本語CCGBankの再構築
- Kubota et al. (2020; LREC) による ABCTreebank
- 日本語CCGBank。
- Noji and Miyao (2016; ACL)
- 日本語CCG parserの Jigg。
- Martinez-Gomez et al. (2016; ACL)
- 意味解析システムの ccg2lambda。
- Bekki and Kawazoe (2016; LNTCS)
- 日本語CCG parserの lightblue。
- Yoshikawa et al. (2017; ACL)
- 日本語CCG parserの depccg。
人間の文処理関係
- Ades and Steedman (1982; Linguist Philos)
- 一番最初のCCG論文。
- 当初より逐次的な文処理を意図して作っていることが明確で良い。
- notationは今とところどころ異なる。
- Demberg (2012; TAG+)
- CCGの逐次的な構造構築に関して、統語論・心理言語学の知見から(否定的に)述べられている。
- CCGではfull incremental parseができない(英語の目的語関係節)。
- full incremental parseを実現しようとDコンビネータを導入すると過剰生成する、という指摘。
- Stanojevic et al. (2023; Cognitive Science)
- CCGによる、英語文処理(fMRIによるBOLD信号)のモデリング。
- 貢献は大きく分けて2つ。
- CCGが、CFG(文脈自由文法)よりもより高い精度でBOLD信号を予測できることを示した。言語理論としてより妥当なCCGが、逐次的な文処理のモデル化においても優れていることを示した。
- CCGの構造構築操作由来の予測子と、LLMで算出したsurprisal(文処理における強力な予測子)とは別にBOLD信号の予測に効いた。
- Kajikawa et al. (2024; CogSci)
- 日本語と英語の視線計測データで、CCG内の理論的に異なる文法操作が、それぞれ心理的にも異なるものとして使われていることを示唆。
- Isono (2024; Cognition)
- 文を逐次的に理解する際に起こる、短期記憶に由来する処理負荷を、CCGの木構造ベースで説明したもの。
- 貢献・面白い点は、短期記憶由来の処理負荷は、今まで簡単な文脈自由文法(記述力は妥当ではない)や依存文法(単語間関係の記述は優れているが、逐次的に構造がどう構築されるかは不明瞭)でしかなかったが、それをCCG (記述力が妥当かつ、構造構築過程も明確) に発展させたこと。
- 個人的に、CCGの良さは、単に「competence grammarのままでprocessingのことをちゃんと語れそうな理論」、ということだけではなく、「いろいろなことができすぎない理論」だと思っています。具体的に、ここでは、構成素同士の合成にちゃんと制限があって、必ずしも何でも組合せられるわけではないが(つまり、単語が順に入ってきたとき、毎度毎度その単語をすでに作っている構成素に統合できるとは限らない)、この論文では、その組合せられないポイントを証拠に人間の文処理が説明できることが経験的に示されています。
生成力関係
- Vijay-Shanker and Weir (1994; Math. Systems Theory)
- CCGの弱生成力が、Linear-Indexed Grammar (LIG), Head Grammar (HG), Tree-Adjoining Grammar (TAG) と等価であることを示した。
- Kuhlmann et al. (2015; CL)
- Vijay-Shanker and Weir (1994) のときに想定されていたCCGではなく、slash-typeを導入したCCGにて、TAGと弱生成力が等価であることを示した。
- Schiffer and Maletti (2021; TACL)
- CCGの強生成力が、TAGと等価だと主張。
標準形関係
- CCGでは、同じ意味を複数の異なる統語構造で表現することができます(spurious ambiguity; 擬似的曖昧性)。このおかげで、逐次的な合成による構造構築が可能なのですが、構造的曖昧性がなくとも構文木が一意に定まらないということなので、parserを作る上では問題になると考えられていました。
- 実際には、学習データのbranchingが一貫していれば、標準形の制約なしでも擬似的曖昧性の問題にはぶつからないようです。Yoshikawa et al. (2017; ACL) や Yoshikawa et al. (2019; 自然言語処理) を参照ください。
- (形式的な研究においては、昔から「避けるべきもの」とされてきていますが、逐次的な文処理という観点からは、むしろ「望ましいもの」でさえある気はしています。直観です。)
- 標準形の定義により、(構造的曖昧性がないとき)統語構造を1つに絞ることができます。
- Eisner (1996; ACL)
- 証明に関する情報
- 可能な限り関数合成(function composition)を行わないという制限により、right-branchingな標準形を定義。
- もちろん、逆の制限にすれば、left-branchingを標準形とすることもできる。
- Hoyt and Baldridge (2008; ACL)
- Dコンビネータの導入と、それを含めた標準形の定義。
- Hockenmaier and Bisk (2010; COLING)
- Eisner (1996; ACL) の拡張。
- generalized compositionとgrammatical type-raisingを考慮した拡張。
言語獲得モデリング
- Piantadosi et al. (2008; Proc. CogSci)
- Bayesian model 1
- Kwiatkowski et al. (2012, EACL)
- Bayesian model 2
- Abend et al. (2017, Cognition)
- Bayesian model 3
CCG parserを触ってみよう!
- CCGは、他の文法理論に比べ、高精度な構文解析器(parser)が数おおく整備されている、という点で非常に有用です。
- semantic parsingに適度に使いやすいといったことや、ツリーバンクの整備が早かった、という点が要因な気がしています(C&C parser が出た頃の2000年代の雰囲気を知らないので妄想です)。
- 特に、下記のparserたちは動かすのにそこまで難易度が高くないのでおすすめです。
- そもそも構文解析器とはなんぞやという方へ。
depccg
- Pythonによる英日CCG parser。
- Python@3.6以上、gcc@4.8以上が必要。
READMEが丁寧なので、基本そのまま従えば動かせる。- 1点だけ、
depccg_{en/ja} downloadコマンドはうまくいかないので、モデルの学習済みパラメータはリンク先のGoogle Driveから直接落としてこないといけない。
- 1点だけ、
- os によっては AllenNLP がローカルで動かせない(本当に動かせないのかわからないが、私は解決できなかった)。
- 2019年のmacbook (Retina) では動かせていたのだが、2023年以降のものではことごとく失敗。
- Dockerを使えば良い。
lightblue
- Haskellによる日本語CCG parser。
- Macユーザーなら、tidyは(おそらく)初めから入っているし、JUMAN++はHomebrew経由で入れられる。
- 戸次 (2010) +アルファがそのまま実装されているので、語彙項目を参照するのに使い勝手が良い。
ccgtools
- Python, Cythonによる英中CCG parser。
- 高性能。元State-of-the-Art。
- 作成者であるMilos Stanojevic氏は、Scalaで Rotating-CCG というparserも作っている。論文は Stanojevic and Steedman (2019; NAACL)。
- Google Colab上で動かせるようにしてくれているので、環境構築の必要がなく非常に便利。
- pre-trained modelのパラメータをダウンロードさえしておけば、ローカルで動かすことができる。
CCGの導出木をLaTeXでかく
ccg.sty
- Jason Baldridge氏によるスタイルファイル。
- その他、CTL, 証明木用のスタイルファイルも公開してくれている。
- 使い方:
ccg.styをTeXファイルと同じディレクトリにおき、以下のようにする:\documentclass[border=2mm]{standalone} \usepackage{amsmath} \usepackage{ccg} \begin{document} \deriv{3}{ \text{Taro} & \text{likes} & \text{Hanako} \\ \uline{1} & \uline{1} & \uline{1} \\ \mathit{NP} & \mathit{S\bs NP/NP} & \mathit{NP} \\ & \fapply{2} \\ & \mc{2}{\mathit{S\bs NP}} \\ \bapply{3} \\ \mc{3}{\mathit{S}} } \end{document}すると↓こんなのができます:
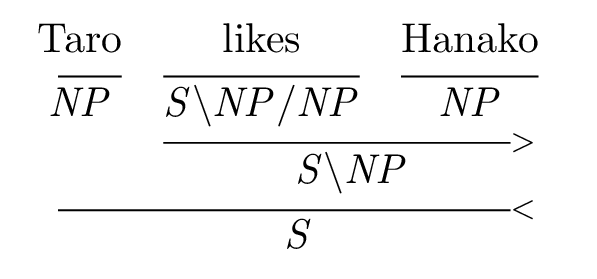
- 導出木のサイズを変えるのには、
\deriv{hoge}{fuga}の前にたとえば\scriptsize\deriv{hoge}{fuga}のようにする。 linguexパッケージで文番号をつける:\ex.\label{hoge-label} \deriv{hoge}{fuga}ulemパッケージ(下線とか打ち消し線を挿入する用のパッケージ)を入れると、ccg.sty内の\uline{}が衝突してしまう。- コマンドの名前が一致していなければ良いだけなので、ccg.styに
\newcommand{\ulines}[1]{\ul{#1}}などと追加して、\deriv内では\ul{}を使うようにすれば良い。
- コマンドの名前が一致していなければ良いだけなので、ccg.styに
ccg-latex.sty
- Cem Bozsahin氏によるスタイルファイル。
- 上述のccg.styよりも充実していそうに思われる。少なくとも、READMEやexampleは充実している。更新も割と頻繁にしているよう。
個人的には、
ccg.styで困っていないので使っていないが、いつか乗り換えてみたいなぁとは思っています。なんだかこだわりを感じるので。- そのほか、証明図を書く
bussproofsを使う、というのもあります。