弱文脈依存文法にまつわる理論言語学のはなし
Published:
自然言語の文法とその生成力に関する話。チョムスキー階層 (Chomsky Hierarchy) や弱文脈依存文法 (Mildly Context-Sensitive Grammars; MCSGs) について、など。
自然言語の形態論・統語論を考えるとき、それらがどの程度「複雑」なのかを考えることは、言語理論を考えるのにも、文産出・理解について考えるのにも、言語獲得について考えるのにも、そして言語進化について考えるのにも極めて重要でしょう。
そして、自然言語の文法の「複雑さ」(以降、適当に「文法」といってしまいます)について、形式言語の世界では「生成力」という概念での整理がなされており、言語学研究としてきちんと扱えると大変嬉しいものだと思います。
というのも、生成力の議論は、何も「自然言語として可能な文字列」について議論したかったから盛んだったわけではなく、人間の瞬時の言語処理をも説明するために不可欠であると、Gazdar et al. (1985) など、指摘されてきていたはずで、必ずしも「数学者や計算機科学の人たちだけが扱えばいいもの」ではないからです。
もちろん、形式文法における parsing complexity と人間の言語処理における parsing complexity が必ずしも一致していないため、両者がすぐさま接続するわけではないとは思いますが。
<工事中>
そもそも、生成力とは?
「生成力(generative capacity)」とは、文法の「複雑さ」の概念です。 ここでの複雑さは、その文法が作る(生成する)ことのできる文字列もしくは木構造をもとに測ることができます。 例えば、2つの文法 \( G_1 \) と \( G_2 \) があり、 \( G_1 \) で作ることのできる文字列はすべて \( G_2 \) で作ることができるのならば、 \( G_1 \) より \( G_2 \) の方が複雑だと思えるでしょう。みたいな感じです。 ここで、文字列に関する生成力を「弱生成力 (weak generative capacity)」と、木構造に関する生成力を「強生成力 (strong generative capacity)」と呼びます (Chomsky, 1965; 福井・辻子, 2017; 日本語訳)。
弱生成力は、ある文法が作ることのできる文字列(単語の配列)の集合に関する概念です。 弱生成力が等しいかつ語彙が等しい文法同士では、作ることのできる文字列の集合は完全に一致します。 生成できる文字列の観点での複雑さのクラス分けとして、チョムスキー階層 (Chomsky hierarcy)(下図。図はJager and Rogers (2012, p.1959)より。)という概念が広く用いられています(Chomsky (1956); Chomsky and Schutzenberger (1963))。
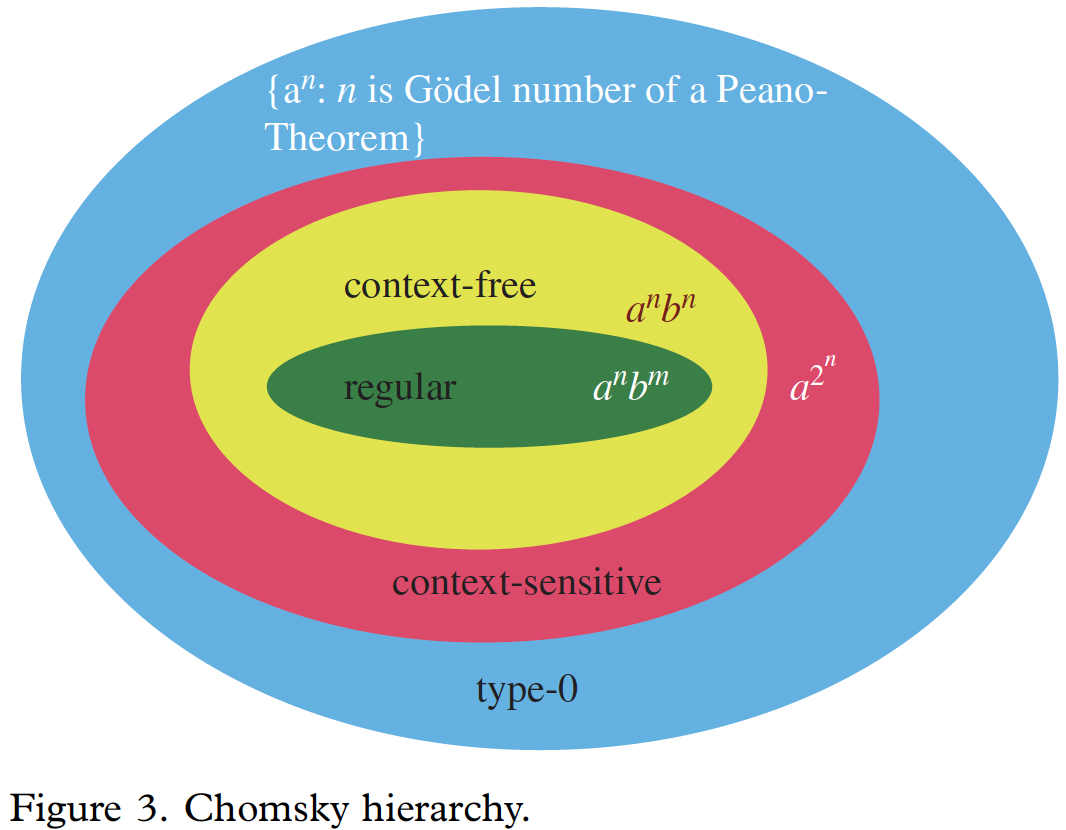
自然言語の弱生成力に関して、詳しくは Jager and Rogers (2012) や Hunter (2020) のレビューを参照ください。 また、計算機科学での言語理論については、関・鯵坂 (2011) が丁寧な解説をしてくださっています。
強生成力は、ある文法が作ることのできる木構造の集合に関する概念であり、Chomsky自身は弱生成力ではなく強生成力を研究の対象とするべし、としました (Chomsky, 1965)。 単に単語をどう配列するのか、ということではなく、その背後にある(音や意味と関わる)階層的な構造の研究が大事なはずでしょう、ということです。 ただ、強生成力それ自体に明確な定義があるわけではなく、そのために理論中立的な議論が難しくなっている、というのが現状です。 というか、「構造」を理論中立的にうまく定義できていないので、強生成力の議論は形式的にはあまり行われていません。 一方で、「強生成力」ということばを使ってはいませんが、一応主流生成文法の人たちは現在に至るまで、強生成力に関する研究を志向しているように見えます。 形式的ではないために反証可能性がない議論が多々潜んでいますが。
もちろん、強生成力についての議論はまったくないわけではなく、最近では、CCGs (Combinatory Categorial Grammars) と TAGs (Tree Adjoining Gdrammars) が弱生成力だけではなく、強生成力においても等価である、と主張されています (Schiffer and Maletti, 2021)。 ここで、では CCGs と TAGs に優劣がないのか、となるとそうではなく、仮にこの2つがまったく同一の文字列・構造を生成するとしても、その過程 (derivation step) は異なるので、そこでどちらの方ががより妥当か、という話になります。
文脈自由文法 (Context-Free Grammars)
弱文脈依存文法の話に行く前に、比較的単純ながら使い勝手の良い文脈自由文法を見てみましょう。
文脈自由文法とは、\( (\Gamma, \Sigma, S, R) \) の4つ組で定義されます。
- \( \Gamma \): 非終端記号の集合
- \( \Sigma \): 終端記号の集合で、\( \Gamma\cap \Sigma=\varnothing \)
- \( \mathit{S}\in \Gamma \): 開始記号
- \( R \): 規則(生成規則)の集合。各規則は、\( \alpha\rightarrow\beta \) の形をとる。
- ここで、\( \alpha\in\Gamma \) はちょうど1つの非終端記号、\( \beta \) は \( (\Gamma\cup\Sigma)^* \) の任意の列(空列を含む)であり、\( \rightarrow \) は左側の要素から右側の要素への書き換えを意味します。
急に記号だらけでイメージがつきにくい、という方は、四則演算を思い出してみましょう。 簡単に、\( 0, 1, \dots, 9 \) の整数による足し算は、以下のようにして書くことができます。
- \( \Gamma = E \)
- \( \Sigma = \lbrace +, 0, 1, \dots, 9\rbrace \)
- \( E \)
- \( R \): \begin{align} E &\rightarrow E + E \newline E &\rightarrow 0 \mid 1 \mid 2 \mid 3 \mid 4 \mid 5 \mid 6 \mid 7 \mid 8 \mid 9 \end{align}
この文法により、1 + 1 も 2 + 3 + 4 も 8 + 9 も書くことができます。+ 8 9 は非文法的な表現ですね。 我々は知らず知らずのうちに文脈自由文法を使っているのです。
「文脈自由」とは、書き換えが非終端記号1つのみに依存し、他の要素から影響を受ける(書き換えに文脈が存在する)というわけではない、という意味です。 例えば、ある文脈自由文法で以下のような導出がされたとすると、\( B \) の書き換えが、\( A \) や \( C \) の状況によって決まる、なんてことはない、ということです。
A
/ \
B C
/ \ / \
d e f g
もう1つの文脈自由言語の特徴として、これは「文脈自由」であることから当然なのですが、ネストした句・構造のみを作ることができます。 どの句も、(親を除く)他の非終端記号の子供たちをその中に混ぜることはありません。 そのため、文脈自由文法によって導出された文脈自由言語の構造は、かっこ () を使って書くことができます。 (3 - (1 + 2)) のようにです。
反復補題
ある言語が文脈自由ではないことは、文脈自由文法の反復補題 (Pumping Lemma) を使うことで示すことができます。 「反復」とは、部分文字列の繰り返しのことを指し、反復補題は、あるクラスに属する形式言語ならば、その部分文字列の一部を繰り返しても引き続きそのクラスに属する、といったことを満たす条件を表します。 とくに、文脈自由文法の反復補題は、自然言語の文法が文脈自由文法で書けるのか?という問題に直接関わる、というか、自然言語の文法が文脈自由文法では不十分であることを示すのに使うので、言語学者にとっても無関係ではないものです:
任意の文脈自由言語 \( L \) について、十分に長い文字列 \( w \in L \) は、\( u,v,x,y,z \in \Sigma^* \) (\( \Sigma^* \) は終端記号列の集合を指す)を使って \( w=uvxyz \) と分解でき、このとき、\( |vy|\geq 1 \) と、ある整数 \( p \) について \( |vxy|\leq p \) であり、次を満たす:
- 任意の \( i\geq 0 \) に対して、\( uv^ixy^iz\in L \)
例として、\( L = \lbrace a^nb^nc^n\mid n\geq 0\rbrace \) が文脈自由言語ではないことを、この反復補題を用いて示してみましょう。
まず、言語 \( L = \lbrace a^n b^n c^n \mid n \geq 0\rbrace \) が文脈自由であると仮定してみましょう。 文脈自由言語の反復補題によれば、ある正の整数 \( m \) について、文字列 \( w = a^m b^m c^m \) が、
\[w = uvxyz\]に分割できるうえ、\( |vy| \geq 1 \) と \( |vxy| \leq m \)、さらに、任意の \( i \geq 0 \) に対して \( uv^i x y^i z \in L \) を満たします。
すると、\( |vxy| \leq m \) より、区間 \( vxy \) としてありえるのはありえるのは、以下の5通りです:
- すべて \( a \)
- \( a \) と \( b \) にまたがる
- すべて \( b \)
- \( b \) と \( c \) にまたがる
- すべて \( c \)
どの状況でも、\( i \geq 2 \) のとき、\( uv^i x y^i z \) で、\( a,b,c \) の記号の数が等しくなりません。
したがって、\( L \) が文脈自由言語であるという仮定は誤りであり、
\[L = \{a^n b^n c^n \mid n \geq 0\}\]は文脈自由ではない言語であることがわかります。
他の文法形式との等価性
projective dependency tree
依存構造木において、依存関係同士が「交差」しないものを ‘‘projective’’ なtreeであるといいます。 文脈自由文法で表現できる依存関係は、projectiveな依存関係にとどまることが知られています。
AB grammar
範疇文法 (Categorial Grammar) において、関数適用しかない範疇文法は、文脈自由文法とその弱生成力が等価です。
自然言語は文脈自由文法で扱えるのか?
では、自然言語は、文脈自由文法で表現することはできるのでしょうか。
三単現の s
まず、文脈自由文法にとって弱点でありそう、と考えられるのは、文脈自由性により「構造依存性 (structure dependence)」を表現できないのではないか?ということです。 構造依存性とは、自然言語の文法は階層的な統語構造に対して適用される、というもので、例えば The walks の s は、主節の主語と動詞をもとに適用されるもので(そして主節の主語・動詞は統語構造からわかるもので)、「一番文頭よりの動詞」のような線形順序に由来するわけではないことは、The man [who played the guitar] walks からわかります。
で、文脈自由文法だと、文脈自由なので、こうした構造上の依存関係を取り扱うのが難しいように思えます。 しかし、何とか解決策はあるもので、それは、例えば「三人称・単数・現在」のような情報を非終端記号に非終端記号に取り込んでしまえばよいのです。
つまり、 \begin{align} \mathit{S_{3,s,pres}} &\rightarrow \mathit{NP_{3,s,pres}}\ \mathit{VP_{3,s,pres}} \newline \mathit{S_{3,p,pres}} &\rightarrow \mathit{NP_{3,p,pres}}\ \mathit{VP_{3,p,pres}} \newline \mathit{NP_{3,s,pres}} &\rightarrow \text{The man} \newline \mathit{NP_{3,p,pres}} &\rightarrow \text{The men} \newline \mathit{VP_{3,s,pres}} &\rightarrow \text{walks} \newline \mathit{VP_{3,p,pres}} &\rightarrow \text{walk} \end{align} のようにして、三人称単数現在 \( _\mathit{3,s,pres} \) と三人称複数現在 \( _\mathit{3,p,pres} \) を分けてやれば良いのです。
ただ、これは美しくない解決策です。 というのも、確かに文法的に正しい文を生成することはできるのですが、このような戦略を取り続けると、文法が大きくなりすぎてしまう可能性があります。 文法はまず「すべての文法的な文を正しく記述でき、非文法的な文は排除できるか」という記述的妥当性に関する側面と、さらには「その文法は合理的なサイズをしているのか」という説明的妥当性に関する側面の両方を満たす必要があります。 その点で、文脈自由文法は少なくとも上記の例を見ると、説明的妥当性において疑わしいように思えます。
とはいっても、説明的妥当性は、現状絶対的な評価は難しく、相対的な評価にとどまるので、記述的妥当性のみでは優劣がつかないような文法の候補が複数現れたときにはじめて検討する、というのが望ましいでしょう。 そのため、もっと明確に記述的妥当性の観点のみで文脈自由文法の妥当性が判断できるような例があれば喜ばしいです。
ここで、文脈自由文法がネストした構造を作る、ということを思い出してみると、自然言語に依存構造がネストではなく交差する現象があれば、その構造は文脈自由文法では取り扱えない、ということがわかります。 では、依存構造が交差する状況は自然言語に存在するのでしょうか?
Respectively読み
依存関係が交差している現象として、respectively を使った文はどうでしょうか。
英語だと、John and Mary walked and ran, respectively という文の意味は、John walkd and Mary ran と同じであり、それぞれ John と walked、Mary と ran の間に意味的な関係があります。 
日本語でも同様です。 太郎 と 次郎 が それぞれ 走り 散歩した では、「それぞれ」をはさんで、主語と述語の間の意味的な関係が交差しています。
この現象は、比較的身近なものだからか、古くから「自然言語が文脈自由文法では扱えきれない証拠」として有名で、今でもしばしば言及されます。 初出は Bar-Hillel and Shamir (1960) です。 しかしながら、この例は文脈自由文法の非妥当性を主張するのには不十分です。 これは、Pullum and Gazdar (1982, pp.481–485) により指摘されているのですが、彼らの主張は至極単純で、respectively読みは単に統語の問題ではなく意味 やそれ以上の問題でしょう、というものです。
これは、たとえば、 The woman and the men walks and run respectively. は文法的でなく、walk and run としないといけない、ということや、 I met the two students. They are from Tokyo and Seoul respectively. のように、主語述語の数は一致させる必要がない上、その respectively で対応する内容は文脈から推察される、 ということが根拠になります。
依存関係が交差していて、さらにそれは統語的なものである、ということを示さない限り、自然言語の文法が文脈自由では不十分、という主張の根拠にはなりません。
Extraction / Scrambling
では、英語の extraposition や 日本語やドイツ語の scrambling(かき混ぜ)はどうでしょうか。
Extraposition from NP とは、たとえば The man walked who played the guitar のような文で、The man [who …] の who 以下関係節がまるまる文末に行き、間に動詞句 walked が入っている構造です。 ここにさらに yesterday なんてのを文頭に追加してあげると、Yesterday the man walked who played the guitar は交差依存を作ることができます。 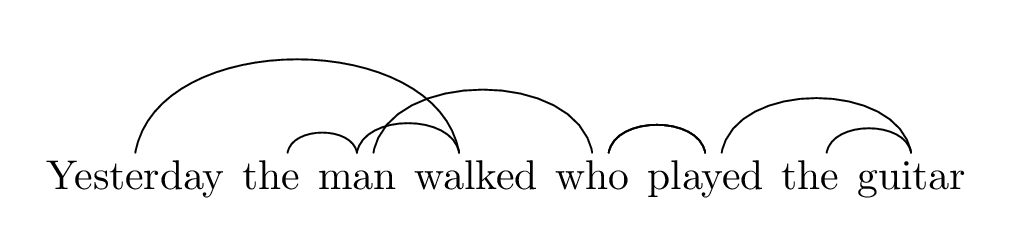
Scramblingは、日本語でよくある、 本を花子が買った。 のような、名詞句の語順が通常の が–を の語順と入れ替わった状態のものです。 日本語は SOV 語順で、動詞の項はすべて NP1 NP2 NP3 V のように動詞に対して同じ方向の位置に並ぶので、NPの順番を並び替えても依存関係は交差しませんが、NPが節境界を超える長距離かき混ぜ (long-distance scrambling) を考えてみると、交差依存を観察することができます。
例えば、目的語コントロール(のような)動詞と組み合わせて、本を 太郎が 花子に 買うよう 頼んだ とすると、この文は交差依存をもちます。 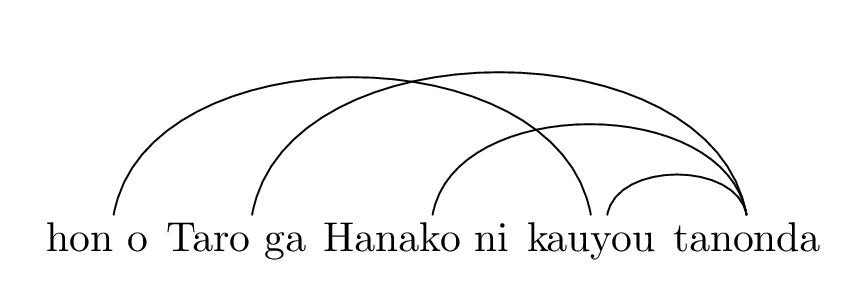
日本語 Universal Dependencies (浅原ら, 2019) だと、「頼む」は「買う」に対して ccomp ラベルの関係をもちます。
* コントロールかもしれない、みたいな変な例文を考えずに、素直に、本を_i 太郎は [花子が t_i 買ったと] 思った みたいな例文を考える、というので良かったかもですね。
こうした交差依存は、さすがに統語的な依存関係であるといえるでしょう。 ただ、こうした例では、依存関係が交差はするのですが、高々有限回であり、構文として文脈自由規則に書いておけば何とか対応はできます。 単語を増やして交差数を増やしてみようと頑張っても、英語や日本語ではネストした埋め込みしかできないので、交差を無限に増やすことができません。 [花子が 太郎に [次郎に [三郎に 本を 買うよう 頼むよう] 頼むよう] 頼んだ] のようにネストしてしまい、交差は増えません。
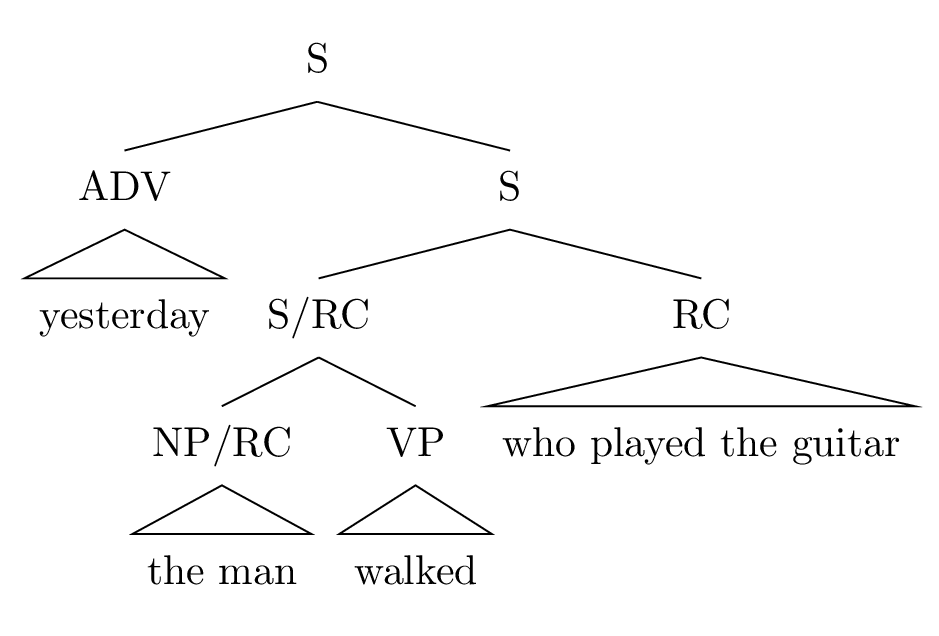
そのため、これらの例もまた、自然言語の非文脈自由性を主張するのには十分ではありません。 例えば extraposition だと、 \begin{align} \mathit{S} &\rightarrow \mathit{S}/\mathit{RC}\ \ \mathit{RC} \newline \mathit{S}/\mathit{RC} &\rightarrow \mathit{NP}/\mathit{RC}\ \ \mathit{VP} \end{align} と、Gazdar (1981) や Gazdar et al. (1985) による Generalized Context-Free Grammar のように、統語的な関係をタグの表現の中に入れてしまえば文脈自由規則のみで扱うことができます。 ここで、\( \mathit{X/Y} \) は「右側に\( \mathit{Y} \) があったら \( \mathit{X} \) になるもの」を表します。
Cross-serial dependencies
ということで、依存関係が統語的に交差してかつ、その交差が連続して無限回繰り返すことのできるするような現象が自然言語にあるのか?ということが問題です。 もったいぶりましたが、紆余曲折を経て、結局文脈自由文法では上手く扱えない「統語的な連続交差依存 (cross-serial dependencies)」が80年代にようやく「発見」されました。
それは、Swiss-German(スイスドイツ語)の従属節中には現れる動詞と対応する項の依存関係です。 Shieber (1985) は、これにより自然言語には文脈自由文法では作れない表現が存在することを示しました。 文は Shieber (1985) より。

動詞列 \( \mathit{V}_1 \cdots \mathit{V}_n \) が文末に連続し、それぞれの目的語列 \( \mathit{NP}_1 \cdots \mathit{NP}_n \) と依存関係を結びます。 Swiss-German では、名詞句(目的語)に dative や accusative の格表示をするので、依存関係が意味的にだけではなく統語的にも交差している、ということがいえます。
同じ意味の文を日本語で表そうとすると、依存関係は交差せず、入れ子構造になります。 
そして、Swiss-German の母語話者ではないので正確なところは分かりませんが、動詞部分で let let let … let help help … help paint と繰り返すと、この動詞の数だけ、対応する名詞を連続させることができます。 つまり、\( a^nb^mc^nd^m \) のような部分文字列が作られます。 これはまさに文脈自由文法では扱えない文字列です。
同様の構文はオランダ語でもあり、Shieber 以前にも Huybregts (1976) や Bresnan et al. (1982) によって非文脈自由性は主張されていたのですが、オランダ語では、Swiss-German とは違い、対角・与格形態的な格表示がないため、必ずしも統語的な交差依存とは考えられず、項の意味的な選択制限を除けば、可能な文字列自体は文脈自由文法で扱える、と主張されていました (Pullum and Gazdar, 1982, pp.485–490)。
なお、同時期に Culy (1985) にて、西アフリカの Bambara を用いて、形態的にも文脈自由文法で表現できない事例が存在すると説明されています。 さらには、Bambara の例は音調的な振る舞いに依存しており、形態論の問題なのか?、という議論があるようで、Sanuma and Aizawa (2024) で、アイヌ語にて形態論レベルでのbeyond context-freenessが示されたようです。
また、Stabler (2004) では、英語においても連続交差依存はあると主張されています。 画像は Stabler (2004; p.701) より。

cross-serial dependencies自体は確かに頻度は多くはないですが (e.g., Ferrer i Cancho et al., 2018)、存在しないわけではないので、自然言語の文法を文脈自由文法で済ますのは不十分であるといえます。
多重文脈自由文法 (Multiple Context-Free Grammars)
自然言語の統語現象を扱うのに文脈自由文法では不十分だとして、ではどうすれば良いのでしょうか。 文脈自由文法を自然に拡張する方法として、多重文脈自由文法 (Multiple Context-Free Grammars; MCFGs; Seki et al., 1991) が提案されています。 MCFGs は、文脈自由文法では単一の文字列としてしか扱えなかった非終端記号を、複数の文字列を束ねたタプルとして扱います。
説明のために、新たな記法を導入します。 いま、文脈自由文法で、\( \mathit{NP} \) という非終端記号が最終的に the man という文字列に派生可能であるとき、\( \mathit{NP}(\textit{the man}) \) と書くとします。 ある文字列 \( x, y \) について、\( xy \) を \( x, y \) の結合だとすると、文脈自由規則は
\[\mathit{NP}(xy)\rightarrow \mathit{D}(x) \ \mathit{N}(y)\]とかけます。
CFGs ではある非終端記号が同時に扱える文字列の数は1つですが、MCFGs ではこれを複数に拡張します:
\[A(x_1,x_2,\cdots,x_k)\rightarrow B(y_1,\cdots,y_n)\ C(z_1,\cdots,z_m)\]The man walked who played the guitar のような extraposition は、以下のようなルールで扱えます: \begin{align} \mathit{S}(xzy)&\rightarrow \mathit{NP}(x,y) \ \mathit{VP}(z) \newline \mathit{NP}(x,y)&\rightarrow \mathit{NP}(x) \ \mathit{RC}(y) \end{align}
MCFGs は、一度に展開できる非終端記号の最大数を rank \( r \)、各非終端記号が同時に扱える文字列の数を dimension \( d \) と呼ぶとすると、 長さ \( n \) 文を \( \mathcal{O}(n^{(r+1)d}) \) のオーダーで認識可能です。 つまり、上記のような extraposition を簡潔に扱えるようなものだと、\( r = 2, d = 2\) となり \( \mathcal{O}(n^6) \) で、Chomsky標準系の CFGs だと \( r = 2, d = 1\) となり \( \mathcal{O}(n^3) \) です。
MCFGs のちゃんとした定義や議論の解説については、関・鯵坂 (2011) や Clark (2014) を参照ください。
自然言語は弱文脈依存言語なのか?
これまでで、自然言語の統語現象を扱うのに文脈自由文法以上の生成力のクラスの文法が必要であることがわかりましたが、では、自然言語の文法はどのクラスに位置するのでしょう。
Joshi (1985) は、自然言語の文法は文脈自由以上、文脈依存以下の弱文脈依存 (mildly context sensitive) クラスに位置する、という仮説を提示しました。
なお、自然言語の文法が弱文脈依存文法(Mildly Context-Sensitive Grammars; MCSGs)であるということは明確に示されているわけではありませんが、少なくとも以下の2つの事実から、「自然言語の文法は弱文脈依存文法である」という言説には一定の合意が得られています。 そのため、しばしば弱文脈依存仮説(MCS Hypothesis)などとも呼ばれています。
1. 文脈自由文法では表現できない構文が自然言語に存在する。
これは、Swiss-German での cross-serial dependencies の議論により示されました。 自然言語を扱うのに必要な文法の lower bound が文脈自由文法ではない、ということがわかっています。
2. 数多くの(独立に提案された)文法理論が、弱文脈依存文法である。
Joshi et al. (1975) による Tree Adjoining Grammar(TAG; 木接合文法)をはじめ、多くの文法理論が、特に80-90年代にかけて、計算・数理言語学の分野で提案されましたが、そのほとんどが最終的に文脈自由文法と文脈依存文法の間にいることが示されました。 これは、多くの計算・数理言語学者の間である種の「合意」がとれた状況とも言えるでしょう。
これについては、Stabler (2013) にてわかりやすくレビューされていますので、少々長いですが引用して提示しておきます。
In particular, a very significant computational consensus was identified by Joshi (1985) in his hypothesis that human languages are both strongly and weakly mildly context sensitive (MCS). While any empirical test of this hypothesis still depends on a network of theoretical assumptions, the claim is so fundamental that it can be connected to many diverse traditions in grammar. To say that language is ‘‘strongly and weakly’’ MCS is to say that MCS grammars can both define the sentences of human languages (weak adequacy) and also provide the structures of those languages (strong adequacy). Joshi’s original definition of MCS grammars was partly informal, so there are now various precise versions of his claim. One is that human languages are defined by tree adjoining grammars (TAGs) or closely related grammars, and another theoretically weaker (and hence empirically stronger) position is that human language are definable by the more expressive (set local) multi-component TAGs or closely related grammars. The most remarkable thing about this claim came out of the innocent-sounding phrase ‘‘or closely related grammars,’’ because it was discovered that a wide range of independently proposed grammar formalisms falls under that description. In particular, a series of papers beginning in the 1980’s and 1990’s established the following inclusion relations among the languages defined by various kinds of grammars, across traditions: CFG ⊂ CCG = TAG ⊂ MCTAG = ACG = MCFG = MG ⊂ CSG
上記引用にて、
- CFGはContext-Free Grammar(文脈自由文法)
- CCGはCombinatory Categorial Grammar(組合せ範疇文法)(Ades and Steedman, 1982; Steedman, 1996)
- TAGはTree Adjoining Grammar(木接合文法)(Joshi et al., 1975)
- MCTAGはMulti-Component Tree Adjoining Grammar (Joshi, 1987)
- ACGはAbstract Categorial Grammar (de Groote, 2001)
- MCFGはMultiple Context Free Grammar(多重文脈自由文法)(Seki et al., 1991)
- MCFGは Linear Context Free Rewriting System (LCFRS; Vijay-Shanker et al., 1987) と同一。
- MGはMinimalist Grammar (Stabler, 1997; Stabler, 2011)
- CSGはContext Sensitive Grammar(文脈依存文法)
を指します。
また、このほかにも、
- Head Grammar (HG; Pollard, 1984)
- Linear Indexed Grammar (LIG; Gazdar, 1988)
も、弱文脈依存文法の仲間であることが示されています (Vijay-Shanker and Weir, 1994)。
ただ、ここで面白いのは、弱文脈依存文法は一枚岩ではなく、上記の Stabler (2013) の引用の最後の関係式で表されているように、2つのクラスに分類できます。 具体的に、CCG, TAG, LIG, HGと、MCTAG, ACG, MCFG, LCFRS, MGです(MGにも複数の亜種があります)。
その後の議論については、たとえば Stanojevic and Steedman (2020) や Frank and Hunter (2021) なども。 どういった文字列や構造を生成できるのか、というところだけでなく、どういった順序でその構造を派生するのか、といったところが議論になっています。
もちろん、各文法理論内でも、「どのような操作を仮定するか」で揺れはあるので、上記の関係が必ずしも成り立つとは限りません。たとえばCCGは、slash-typingを導入することで(=組合せ規則の適用に制限をかけることで)、TAGよりも弱生成力が低くなることも示されています (Kuhlmann et al., 2015)。
また、Head-driven Phrase Structure Grammar (HPSG; Pollard and Sag, 1994) やType Logical Grammar (TLG; 適切な引用がわからないのでSEPへ) のような、チューリング完全な文法理論もあります。
弱文脈依存文法の心理的妥当性
弱文脈依存文法による文処理モデリング
上記のような議論ほど有名ではありませんが、最近では、計算心理言語学の分野においても、弱文脈依存文法の文脈自由文法に対する優位性は主張されています。 たとえば、Brennan et al. (2016) や Li and Hale (2019) は MG と CFG を比較して、Stanojevic et al. (2023) は CCG と CFG を比較して、それぞれ MCSGs である MG, CCG の方が、CFG よりも適切に、人が物語を聞いている間のBOLD信号(Blood Oxygen Level Dependent signals; 脳活動を反映した信号)を予測できることを示しました。
もちろん、Hale et al. (2022) で指摘されているように、こうした結果は必ずしも MCSGs が uniquely the right theory of human grammar (Hale et al., 2022; p.12) であるということを意味しているわけではありませんが、MCSGs が、人間の文処理に関して、CFGs では説明できていないところを説明できているのは確かです。
とはいっても、これらの研究だけで「やっぱり文処理において MCSGs クラスの文法を使っているのだ!」と信じるのは多分良くなくて、というのも、人間が文処理において必ずしも常に正確に parsing をしているとも限らない上、同時に複数の文法を使っている可能性もあります。 たとえば、日本語の助動詞の連続だけなら正規文法で記述できるなど、部分部分では必ずしも複雑な文法は必要がない、とか、フレーズや構文は毎度 parse しているのではなく、記憶して使っている、みたいなこともあるでしょう。
また、MCSGs と CFGs の比較などは、基本的には言語現象をもとに議論できるもので、文処理研究において MCSGs を意識することで面白くなるのは、「脳の部位によって異なる文法を異なるタイミングで使っているのか」といった脳内の処理の過程を細かくみる、という研究や、extraposition や scrambling, cross-serial dependencies といった現象の処理がどのようにして行われているのか、という現象を限定した研究においてでしょう。